一种改善微弱信号信噪比的小波变换消噪法
时间：05-14
来源：EDN
点击：
0 引 言
任何一个系统都不可能做到完全没有噪声，甚至有相当多的时候所需要的有用信号被强背景噪声淹没。因此如何从信噪比为负十几dB甚至几十个dB的环境中有效地提取出有用信号显得越来越重要。对于这种微弱信号的检测问题的研究，目前已经取得一些进展，比如随机共振检测理论、分段采样信号的相位关联检测技术以及混沌理论微弱信号检测原理等。虽然各有所长，但在实际运用过程中还存在这样那样的缺陷，不能满足需要。
这里介绍了最近发展较快的小波分析理论在信号去噪方面的应用，提出了适合于极低信噪比条件下的小波变换去噪法，通过构造具有自适应性的阈值函数以及阈值处理方式的优化设计，可以提取微弱的有用信号特征信息，实现信号恢复。
1 小波变换检测微弱信号原理
小波分析是一种时频域分析，具有多分辨率特性。因此在时频域都具有表征信号局部特征的能力，是一种窗口大小不变但其形状可改变时频局部化分析方法。在高频部分使用逐渐尖锐的时间分辨率和较低的频率分辨率，以便移近观察信号的快变部分；在低频部分具有较高的频率分辨率和较低的时间分辨率，以便移远观察信号的慢变部分(整体变化趋势)，小波这种信号分析表示特征对分析非平稳信号是非常有效的，很适合探测正常信号中夹带的瞬态反常现象并且展示其成分。这种时频面上的分析给信号处理带来前所未有的更为深入的发展。
运用小波分析进行一维信号消噪处理是小波分析的重要应用之一，下面将其消噪的基本原理做简要的说明。
一个含噪声的一维信号的模型可以表示成如下的形式：
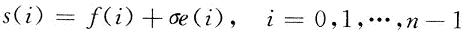
其中：f(i)为真实信号；e(i)为噪声；s(i)为含噪声的信号。在实际工程中，有用信号通常表现为低频部分或是一些比较平稳的信号，而噪声信号则通常表现为高频的信号。所以消噪过程可按如下方法进行处理：首先对信号进行小波分解，则噪声部分通常包含在各层的高频分量中，因而可以以门限阈值等形式对小波系数进行处理，然后对信号进行重构即可达到消噪的目的。
根据上文的分析可以知道，一维信号的消噪过程可分为2个步骤进行：
(1)一维信号的小波分解。选择一个小波并确定一个小波分解的层次N，然后对信号进行N层小波分解；
(2)小波分解高频系数的阈值量化。从第1层到第N层的每一层高频系数选择1个阈值进行软阈值量化处理；
(3)一维小波的重构。根据小波分解的第N层的低频系数和经过量化处理后的第1层到第N层的高频系数，进行一维信号的小波重构。
在这三个步骤中，最关键的就是如何选取阈值和如何进行阈值的量化，从某种程度上说，它关系到信号的质量。这里针对传统信号的阈值函数选取以及分解系数处理方式的不足之处，结合工程实际进行了改善。
2 小波阈值函数的构建
小波阈值去噪的理论依据为：属于能量有限空间的信号在小波域内其能量主要集中在有限的几个系数中，而噪声的能量却分布在整个小波域中，因此经过小波分解后信号的系数要大于噪声的系数，于是可以找到一个合适的数λ作为阈值(门限)，当分解系数小于该阈值时，认为这时的分解系数主要是由噪声引起的，并置为零，予以舍弃；当分解系数大于该阈值时，认为这时的分解系数主要是由信号引起的，则把这一部分分解系数的直直接保留下来(硬阈值方法)或者按某一固定量向零缩(软阈值方法)，然后由新的小波系数进行小波重构到去噪后的信号。
小波阈值的选取是一个非常重要的步骤，其直接影响噪声消除的效果。很明显，如果阈值过高，则会将系数分量中的信号成分当作噪声分量去除，造成信号失真；反之，若阈值选取过低，又不能充分去除噪声，不能达到很好的效果。此外，不同的阈值构建方法其适用场合也不尽相同，必须围绕信噪比和信号特点综合考虑构建方式。
针对微弱信号的特点，即SNR<一1，此时噪声的能量较大，由于信号的信噪比：
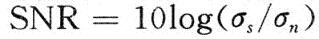
式中：σs为信号强度；σn为噪声强度。由此可知，当信号强度减小或者噪声强度增大时，信噪比均会减小。因此，当噪声占主要地位时，若是只考虑噪声强度是不全面的，例如当信号强度不变，增大噪声，信噪比减小；若是只考虑噪声强度则会使得阈值成线性上升，使得丢失的信息过多，对于信号参数的估计和信号的重构都是不利的。另一方面，如果信号是周期性连续信号，最好选择同样具有连续性的阈值函数。因此，考虑选取阈值为：
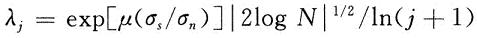
其中：j为小波变换尺度；N为采样点个数；μ为调节因子；用以调节随σs/σn变化，exp[μ(σs/σn)]变化的快慢。
3 阈值处理方式的优化
传统的硬、软阈值方法虽然在实际中得到了广泛的应用，也取得了较好的效果，但这些方法本身还存在一些缺陷。在硬阈值处理过程中，得到的估计小波系数值连续性差，即由于分解系数在±λ处是不连续的，因此重构所得的信号可能会产生一些振荡；而软阈值方法中估计小波系数虽然整体连续性好，但是由于当小波系数较大时，分解系数之间总存在恒定的偏差，这将直接影响重构信号与真实信号的逼近程度，给重构信号带来不可避免的误差。
如果对噪声用分解的系数用C(J，k)表示，其中j代表小波尺度，k代表时间，则可以得出如下结论：
(1)如果所分解的信号是一个平稳、零均值的白噪声，则其小波分解系数是不相关的；
(2)如果所分解的信号是一个高斯噪声，则其小波分解系数是独立的，并且也是高斯分布的；
(3)如果所分析的信号是一个有色、平稳、零均值的高斯噪声序列，则其小波分解系数也是高斯序列。对每一个分解尺度j，其系数是一个有色、平稳的序列。
用ω(j,k)表示对含噪信号进行小波分解后得到的小波系数，由于小波变换是一种线形变换，因此它由2部分组成：信号对应的小波系数和噪声对应的小波系数。由于软阈值方法估计出来的小波系数ω(j,k)的绝对值总比ω(j,k)要小λ而影响了重构精度，应设法减小此偏差。只要使ω(j,k)与由信号对应的小波系数之间的差值尽量小，则ω(j,k)更接近于信号对应的小波系数，重构精度就越高。构造函数：
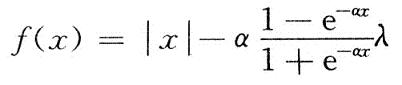
可知，当a=O时上式等效为。Donoho硬阈值；当a一1时，上式等效为Donoho软阈值；当a在0～1之间变化时，z一±cx3，有|f(x)一x|一>aλ。也就是说，随着ω(j,k)模值的增大，ω(j,k)与ω(j,k)偏差的绝对值逐渐减小为αλ，大大减小了软阈值方法中产生的恒定偏差，提高了重构精度，改善了去噪效果。可见，相对于硬、软阈值函数，新阈值函数是一个更优、更灵活的选择。只要在0和1之间适当的调整α的大小，就可以获得更好的去噪效果。图1是用．Matlab画出的Donoho软、硬阈值图及新阈值函数图(α=O．1)。
任何一个系统都不可能做到完全没有噪声，甚至有相当多的时候所需要的有用信号被强背景噪声淹没。因此如何从信噪比为负十几dB甚至几十个dB的环境中有效地提取出有用信号显得越来越重要。对于这种微弱信号的检测问题的研究，目前已经取得一些进展，比如随机共振检测理论、分段采样信号的相位关联检测技术以及混沌理论微弱信号检测原理等。虽然各有所长，但在实际运用过程中还存在这样那样的缺陷，不能满足需要。
这里介绍了最近发展较快的小波分析理论在信号去噪方面的应用，提出了适合于极低信噪比条件下的小波变换去噪法，通过构造具有自适应性的阈值函数以及阈值处理方式的优化设计，可以提取微弱的有用信号特征信息，实现信号恢复。
1 小波变换检测微弱信号原理
小波分析是一种时频域分析，具有多分辨率特性。因此在时频域都具有表征信号局部特征的能力，是一种窗口大小不变但其形状可改变时频局部化分析方法。在高频部分使用逐渐尖锐的时间分辨率和较低的频率分辨率，以便移近观察信号的快变部分；在低频部分具有较高的频率分辨率和较低的时间分辨率，以便移远观察信号的慢变部分(整体变化趋势)，小波这种信号分析表示特征对分析非平稳信号是非常有效的，很适合探测正常信号中夹带的瞬态反常现象并且展示其成分。这种时频面上的分析给信号处理带来前所未有的更为深入的发展。
运用小波分析进行一维信号消噪处理是小波分析的重要应用之一，下面将其消噪的基本原理做简要的说明。
一个含噪声的一维信号的模型可以表示成如下的形式：
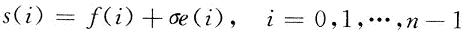
其中：f(i)为真实信号；e(i)为噪声；s(i)为含噪声的信号。在实际工程中，有用信号通常表现为低频部分或是一些比较平稳的信号，而噪声信号则通常表现为高频的信号。所以消噪过程可按如下方法进行处理：首先对信号进行小波分解，则噪声部分通常包含在各层的高频分量中，因而可以以门限阈值等形式对小波系数进行处理，然后对信号进行重构即可达到消噪的目的。
根据上文的分析可以知道，一维信号的消噪过程可分为2个步骤进行：
(1)一维信号的小波分解。选择一个小波并确定一个小波分解的层次N，然后对信号进行N层小波分解；
(2)小波分解高频系数的阈值量化。从第1层到第N层的每一层高频系数选择1个阈值进行软阈值量化处理；
(3)一维小波的重构。根据小波分解的第N层的低频系数和经过量化处理后的第1层到第N层的高频系数，进行一维信号的小波重构。
在这三个步骤中，最关键的就是如何选取阈值和如何进行阈值的量化，从某种程度上说，它关系到信号的质量。这里针对传统信号的阈值函数选取以及分解系数处理方式的不足之处，结合工程实际进行了改善。
2 小波阈值函数的构建
小波阈值去噪的理论依据为：属于能量有限空间的信号在小波域内其能量主要集中在有限的几个系数中，而噪声的能量却分布在整个小波域中，因此经过小波分解后信号的系数要大于噪声的系数，于是可以找到一个合适的数λ作为阈值(门限)，当分解系数小于该阈值时，认为这时的分解系数主要是由噪声引起的，并置为零，予以舍弃；当分解系数大于该阈值时，认为这时的分解系数主要是由信号引起的，则把这一部分分解系数的直直接保留下来(硬阈值方法)或者按某一固定量向零缩(软阈值方法)，然后由新的小波系数进行小波重构到去噪后的信号。
小波阈值的选取是一个非常重要的步骤，其直接影响噪声消除的效果。很明显，如果阈值过高，则会将系数分量中的信号成分当作噪声分量去除，造成信号失真；反之，若阈值选取过低，又不能充分去除噪声，不能达到很好的效果。此外，不同的阈值构建方法其适用场合也不尽相同，必须围绕信噪比和信号特点综合考虑构建方式。
针对微弱信号的特点，即SNR<一1，此时噪声的能量较大，由于信号的信噪比：
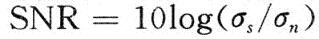
式中：σs为信号强度；σn为噪声强度。由此可知，当信号强度减小或者噪声强度增大时，信噪比均会减小。因此，当噪声占主要地位时，若是只考虑噪声强度是不全面的，例如当信号强度不变，增大噪声，信噪比减小；若是只考虑噪声强度则会使得阈值成线性上升，使得丢失的信息过多，对于信号参数的估计和信号的重构都是不利的。另一方面，如果信号是周期性连续信号，最好选择同样具有连续性的阈值函数。因此，考虑选取阈值为：
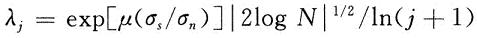
其中：j为小波变换尺度；N为采样点个数；μ为调节因子；用以调节随σs/σn变化，exp[μ(σs/σn)]变化的快慢。
3 阈值处理方式的优化
传统的硬、软阈值方法虽然在实际中得到了广泛的应用，也取得了较好的效果，但这些方法本身还存在一些缺陷。在硬阈值处理过程中，得到的估计小波系数值连续性差，即由于分解系数在±λ处是不连续的，因此重构所得的信号可能会产生一些振荡；而软阈值方法中估计小波系数虽然整体连续性好，但是由于当小波系数较大时，分解系数之间总存在恒定的偏差，这将直接影响重构信号与真实信号的逼近程度，给重构信号带来不可避免的误差。
如果对噪声用分解的系数用C(J，k)表示，其中j代表小波尺度，k代表时间，则可以得出如下结论：
(1)如果所分解的信号是一个平稳、零均值的白噪声，则其小波分解系数是不相关的；
(2)如果所分解的信号是一个高斯噪声，则其小波分解系数是独立的，并且也是高斯分布的；
(3)如果所分析的信号是一个有色、平稳、零均值的高斯噪声序列，则其小波分解系数也是高斯序列。对每一个分解尺度j，其系数是一个有色、平稳的序列。
用ω(j,k)表示对含噪信号进行小波分解后得到的小波系数，由于小波变换是一种线形变换，因此它由2部分组成：信号对应的小波系数和噪声对应的小波系数。由于软阈值方法估计出来的小波系数ω(j,k)的绝对值总比ω(j,k)要小λ而影响了重构精度，应设法减小此偏差。只要使ω(j,k)与由信号对应的小波系数之间的差值尽量小，则ω(j,k)更接近于信号对应的小波系数，重构精度就越高。构造函数：
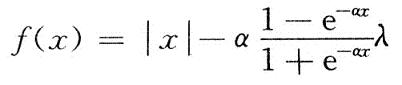
可知，当a=O时上式等效为。Donoho硬阈值；当a一1时，上式等效为Donoho软阈值；当a在0～1之间变化时，z一±cx3，有|f(x)一x|一>aλ。也就是说，随着ω(j,k)模值的增大，ω(j,k)与ω(j,k)偏差的绝对值逐渐减小为αλ，大大减小了软阈值方法中产生的恒定偏差，提高了重构精度，改善了去噪效果。可见，相对于硬、软阈值函数，新阈值函数是一个更优、更灵活的选择。只要在0和1之间适当的调整α的大小，就可以获得更好的去噪效果。图1是用．Matlab画出的Donoho软、硬阈值图及新阈值函数图(α=O．1)。
- 音频系统应用中的“POP”噪声以其常用解决方法(12-01)
- 运算放大器电路固有噪声的分析与测量(第二部分)：运算放大器噪声介绍(05-12)
- 运算放大器电路固有噪声的分析与测量(第二部分)：运算放大器噪声介绍(二)(05-12)
- 运算放大器电路的固有噪声分析与测量(07-14)
- 电源完整性与地弹噪声的高速PCB仿真(05-23)
- 九个步骤大幅降低移动电话非稳态噪声(06-22)
闁诲繐绻愮€氫即銆傞懜鐢碘枖闁规崘灏欓悷褰掓煕閳哄喚鏀版い鏂垮瀵偄鈻庨幋鏃€鐓犻梺瑙勪航閸斿繐鐣烽敓锟�
- 婵°倕鍊瑰玻鎸庮殽閸モ晙鐒婇柛鏇ㄥ灱閺嗐儳鈧鎮堕崕鎶藉煝閼测晜鏆滈柛顐ｇ箓閹鏌熺€涙ê濮囬柣鎾规硶閹峰顢橀悢鍛婄暚缂備礁顑呴鍛淬€冨⿰鍛晳闁跨噦鎷�
闂佺ǹ绻堥崝宥夊蓟閻斿憡濯寸€广儱鎷嬮崝鍛槈閺冨倸孝闁汇劎濮甸敍鎰板箣濠婂懐鎳囨繛鎴炴尰濮樸劑鎮￠敍鍕珰闁糕槅鍘剧粈澶愭煙缂佹ê濮囩€规洖鐭傞幆宥夊棘閸喚宀涢悗瑙勬偠閸庢壆绱為弮鍫熷殑闁芥ê顦～鏃堟煥濞戞ǹ瀚板┑顕呬邯楠炲啴濡搁妷锕€娓愰梻渚囧亞閸犳劙宕瑰鑸碘拹濠㈣埖鐡曠粈瀣归崗鍧氱細妞ゎ偄鎳橀幆鍐礋椤愩倖顔忔俊顐ゅ閸ㄥ灚瀵奸幇顔剧煓閻庯綆浜為悷锟�...
- 婵炴垶鎼╅崢鐐殽閸モ晙鐒婇柛鏇ㄥ灱閺嗐儳鈧鎮堕崕鎶藉煝閼测晜鏆滈柛顐ｇ箓閹鏌熺€涙ê濮囬柣鎾规硶閹峰顢橀悢鍛婄暚缂備礁顑呴鍛淬€冨⿰鍛晳闁跨噦鎷�
缂備緡鍣ｇ粻鏍焵椤掑﹥瀚�30婵犮垼鍩栧畝绋课涢鍌欑剨闁告洦鍨奸弳銉╂煕閳哄喚鏀版い鏂垮閹风娀宕滆閺屻倝鏌ㄥ☉妯侯殭缂佹鎸鹃埀顒傤攰閸╂牕顔忕捄銊﹀珰闁规儳鎳愮粈澶愭煕閺傜儤娅呮い鎺斿枛瀹曘劌螣閻戞ê娓愰梻渚囧亞閸犳洟骞撻鍫濈濡鑳堕鍗炩槈閹垮啩绨婚柟顔奸叄瀵粙鎮℃惔锝嗩啅婵☆偆澧楅崹鍨閹邦喚鐭欓悗锝庝簽閻熷酣鏌ｉ妸銉ヮ伂妞も晪绠戞晥闁跨噦鎷�...
- Agilent ADS 闂佽桨鐒﹂悷銉╊敆閻旂厧鏄ョ痪顓炴媼閸炴煡鎮归崶褍鈷旈柍璇插悑缁鸿棄螖閸曞灚顥�
婵炴垶鎸婚幐鎼侇敊瀹ュ绠抽柛顐秵閸わ箓鏌ㄥ☉妯垮闁告瑥绻樺Λ鍐閿濆骸鏁奸柣鐔哥懐閺嬪儊S闂佸憡鑹剧€氼噣锝為幒妤€绀夐柣鏃囶嚙閸樻挳鏌涘⿰鍐濞村吋鍔楃划娆戔偓锝庝簽鐎瑰鏌ｉ姀鈺冨帨缂侀亶浜跺畷婵嬪煛閸屾矮鎲鹃梺鐑╁亾閸斿秴銆掗崼鏇熷剹妞ゆ挾濮甸悾閬嶆煛閸愩劎鍩ｆ俊顐ユ硶閳ь剚鍐荤紓姘辨閻у挷S...
- HFSS闁诲孩鍐荤紓姘卞姬閸曨垰鏄ョ痪顓炴媼閸炴煡鎮归崶褍鈷旈柍璇插悑缁鸿棄螖閸曞灚顥�
闁荤姍鍐仾缂佽鐒︾粙澶愬箻閹颁礁鏅欓梺鐟版惈閻楁劙顢氶幎鑺ユ櫖閻忕偠妫勫鍧楁⒒閸稑鐏辨い鏂款樀楠炴帡宕峰▎绂⊿闂佹眹鍔岀€氼剚鎱ㄥ☉銏″殑闁芥ê顦扮€氭煡骞栫€涙ɑ鈷掗柡浣靛€濋弫宥囦沪閽樺鐩庨梺鍛婃煛閺呮粓宕戝澶婄闁靛ň鏅滃銊х磼椤栨繂鍚圭紒顔芥そ瀹曠兘寮跺▎鎯уΤ婵炴垶姊绘慨鐢垫暜婢舵劕绠垫い鈥抽敪SS...
- CST閻庣敻鍋婇崰妤冧焊濠靛棭鍟呴柕澶堝€楃粙濠囨倵楠炲灝鈧洟鎮＄捄銊﹀妞ゆ挾鍠愬▓宀€绱掔€ｎ亶鍎忔い銊︾矌閹叉鏁撻敓锟�
闂佸搫顦€涒晛危閹存緷铏光偓锝傛櫅閻︽粓鎮规担绛嬪殝缂佽鲸绻堝畷妤呭Ω閳哄倹銆冮柣鐘辩瀵泛顔忕欢缍璗闂佸憡鑹剧€氫即濡村澶婄闁绘棁顕ч崢鎾煕濠婂啳瀚板ù鍏煎姉缁瑧鈧綆浜炵€瑰鏌ｉ姀鈺冨帨缂佽鲸绻堝畷婵嬪煛閸屾矮鎲鹃棅顐㈡祩閸嬪﹪鍩€椤掑倸鏋欓柛銈嗙矌閳ь剚鍐婚梽鍕暜婢舵劕绠垫い鈥愁敍T闁荤姳鐒﹀畷姗€顢橀崨濠冨劅闁哄啫鍊归弳锟�...
- 闁诲繐绻愮€氫即銆傞崼鏇炴槬闁惧繗顕栭弨銊╂煕閳哄喚鏀版い鏂垮閹风娀宕滆閺岋拷
婵炴垶鎸稿ú锝囩箔閳ь剙螖閸屾惮鎴﹀Χ婵傚摜宓侀柛鎰级閸曢箖鎮硅閸ゆ牜妲愬┑鍥ㄤ氦婵炲棗娴烽弰鍌炴偣閸パ冣挃闁宠鍚嬬粙澶嬫姜閹殿喚鈽夐梺闈╄礋閸斿矂鎯冮悩绛圭矗闁瑰鍋涜灇闂佸搫鐗滈崹鍫曘€傞锕€鏄ラ柣鏃€鐏氭禍锝夋倶閻愬瓨绀冮悗姘辨暬閹虫ê顫濋崜褏顦梺鐟扮仛閹搁绮崨鏉戦敜婵﹩鍓涢弶浠嬫煟閵娿儱顏х紒妤佹尰缁嬪顫濋鍌氭暏缂佺虎鍘搁崑锟�...
- 閻庣敻鍋婇崰妤冧焊濠靛牅鐒婇柛鏇ㄥ灱閺嗐儲绻涢弶鎴剶闁革絾妞介獮娆忣吋閸曨厾鈻曢梺绯曟櫇椤㈠﹪顢欓崟顓熷珰闁告挆鈧弻銈夋煕濮橆剛澧︽繛澶涙嫹
闁荤姵鍔﹂崢娲箯闁秴瑙﹂柛顐犲劜閼茬娀鏌￠崶銊︾稇闁汇倕瀚伴獮鍡涙偑閸涱垳顦紓鍌氬暞閸ㄧ敻宕规惔銊ノュ〒姘ｅ亾妞わ絽澧庨幏顐﹀矗濡搫纾块梺闈涙閼冲爼濡靛顑芥灃闁靛繒濮甸悵銈夋煏閸℃洘顦峰ǎ鍥э躬瀹曪綁鏌ㄧ€ｎ剛鍩嶉梺鎸庣☉閺堫剟宕瑰⿰鍛暫濞达絽婀辨竟澶愭煛瀹ュ妫戠紒銊ユ健閺屽懘鏁撻敓锟�...
栏目分类