DSP+FPGA在高速高精运动控制器中的应用

2 软件设计


该运动控制卡应用时插在工控机的ISA槽上，与上位机配合工作。首先在上位NC机输入加工曲线，由上位机做粗插补，然后把数据通过ISA接口传递给控制卡。控制卡对接收到的数据再做细插补--采用三次B样条插值,然后发送给DA，驱动电机运动。DSP通过FPGA进行脉冲计数，读出直线电机光栅尺的反馈信息，然后采用离散PID控制算法调整，以便于电机运动控制的最优化。

运动控制算法的核心是先用B样条插值法把目标点进一步细化，使运动曲线更平滑，然后在运动过程中采用PID算法进行调整，最终达到高速高精的设计要求，图4给出了系统软件流程图。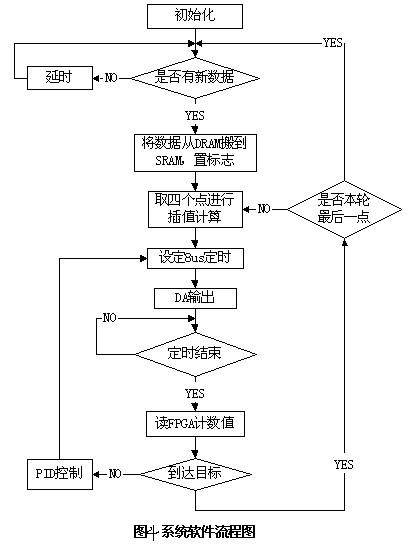


2.1 B样条插值

目前许多先进的CAD/CAM系统都采用了B样条曲线。其特点是，可用统一的数学形式精确表示分析曲线（如直线，圆锥曲线等）和自由曲线（如均匀B样条曲线等），因而便于用统一的数据库管理、存储，程序量可以大大减少；非均匀B样条曲线定义中的权因子使外形设计更加灵活方便，设计人员通过调整具有直观几何意义的点、线、面元素即可达到预期的效果。

本系统采用三次B样条曲线作为精插补算法，该算法应用在控制卡中可以得到比较满意的效果。计算过程中只需要相邻4个点的位置数据,(x0,y0)，(x1,y1)，(x2,y2)，(x3,y3)，就可以构造出平滑的曲线。

公式以坐标分量形式表示为：

2.2 PID控制

在控制领域中，PID控制算法是一种常用的算法，PID是比例、积分、微分的缩写。PID的合理的参数估计、比较，可以通过MATLAB的传递函数模型仿真来得到。

由于该系统是数字系统，采用的都是数字量，所以必须把PID算法离散化才能使用。又由于系统的存储空间有限，算法的存储空间开销不能太大，所以采用了离散化的增量式PID算法。该算法在运算过程中只需要保留最近3次的误差数据，就能够推导出下一次的输出量，节省了大量的数据空间，提高了运算速度，有很强实用价值。

公式如下：

μ( k )，μ( k-1 )分别是k和k-1时刻的输出量，在系统中体现为DA的输出量。
e( k )，e( k-1 )，e( k-2 )分别是k，k-1，k-2 时刻的偏差值，在系统中体现为该时刻实际位置与目标位置的偏差。
T，Td，Ti，Kp是PID公式的常量，不同的数值代表着PID系统的微分、积分、比例调节作用的强度和效果。

3 小结


在开放式数控系统中应用基于DSP+FPGA的运动控制卡，DSP承担了CNC系统中实时性要求较高的模块功能。利用DSP高速运算能力和实时信号处理能力，采用先进的Bs
pline插补算法，使该DSP运动控制卡具有高速、高精度的性能，结合FPGA芯片的先进技术，使该运动控制卡的集成性、可靠性大大提高。本运动控制卡目前是基于ISA总线设计的，今后将考虑把该系统移植到PCI总线上，将能进一步提高系统的处理速度能力，适应更高要求。

参考文献


1 TMS320C3x User’s Guide, Texas Instruments, 2001
2 TMS320C3x General-Purpose Applications, Texas Instruments, 2001
3 孙家广. 计算机图形学. 清华大学出版社
4 解旭辉. 超精机床数控系统与伺服控制技术研究[Ｄ]. 长沙:国防科技大学， 1997
5 来晓岚, 赵佳明, 卢焕章. DSP+FPGA实时信号处理系统, 电子技术应用， 2002.7
6 胡育文, 陈宏, 顾毅康. 基于DSP的电机控制器设计中的几个问题. 中国自动化学会 ,1999.10
7 潘日红, 潘日晶. 周期B样条曲线的快速递推升阶方法. 福建师范大学学报(自然科学版), 2001.4
8 刘金琨. 先进PID控制及其MATLAB仿真. 电子工业出版社, 2003