基于FPGA的卷积码的编/译码器设计

　　卷积码是Elias在1955年最早提出的，稍后，Wozencraft在1957年提出了一种有效译码方法，即序列译码。Massey在1963年提出了一种性能稍差，但比较实用的门限译码方法，由于这一实用性进展使卷积码从理论走向实用。而后Viterbi在1967年提出了最大似然译码法，该方法对存储器级数较小卷积码的译码很容易实现，并具有效率高、速度快、译码器简单等特点，人们后来称其为维特比算法或维特比译码，广泛应用于现代通信中。本文主要论述了基于Xilinx公司的FPGA的卷积编码器及相应的维特比译码器的研究，并在幸存路径存储与译码输出判决方面提出了改进算法，从而使译码器结构得到简化。

　　1 卷积码的编码原理与实现

　　卷积码是一种重要的前向纠错编码FEC，用(n，k，m)表示。分组码不同，其监督元与本组的信息元和前若干组的信息元有关。这种编码的纠错能力强，不仅可纠正随机差错，而且可纠正突发差错。卷积码根据需要，有不同的结构及相应的纠错能力，但都有类似的编码规律。卷积码的编码器是一个具有k个输入位(端)、n个输出位(端)，m级移位寄存器的有限状态记忆系统。通常称为时序网络。其中R=k／n为编码效率，m为约束长度。卷积码编码原理如图1所示。

　　卷积编码充分利用各组信息元之间的相关性，在误码率和复杂度相同的情况下性能优于分组码，并且最佳译码更易实现，因此在通信系统中得到广泛应用。但是卷积码没有严格的代数结构，尚未找到严密的数学手段将纠错性能与码的构成有规律地联系起来，目前大都采用计算机搜索好码。通常是(2，1，3)卷积码，本文以生成多项式G=(111，101)的(2，1，3)卷积码为例介绍设计和实现过程。

　　设初始状态为SO编码为00，根据生成矩阵分别带入输入O和输入1时得到下一个状态和相应输出。依次代入，可得到如图2所示的状态图。

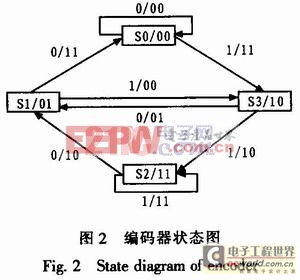
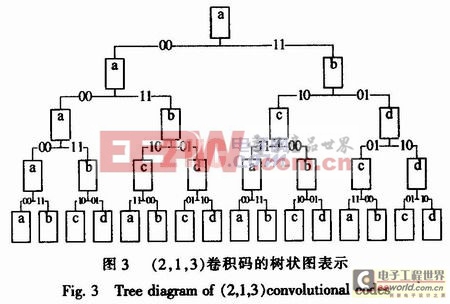
　　描述卷积码的方法主要有两类：图解表示和解析表示。上文提到的生成多项式G=(111，101)即是解析表示。卷积码的图解表示又可分为树状图、网格图和状态图3种。下面介绍常用的树状图表示(网格图表示将在译码部分介绍)。在图2所示的卷积编码树状图中，假设移位寄存器的起始状态全为0，当第1个输入比特为O时，输出比特为00；若输入比特为1时，则输出比特为11。随着第2个比特输入，第1个比特右移1位，此时输出比特同时受当前输入比特和第1个输入比特的影响。第3个比特输入时，第1、2比特分别右移1位，同时输出2个由这3位移位寄存器存储内容所共同决定的比特。当第4个比特输入时，第1个比特移出移位寄存器而消失。移位过程可能产生的各种序列如图3中的二叉树。

　　2 Velerbi(维特比)译码器原理

　　卷积码的译码方式有3种：Veterbi译码、门限译码和序列译码。其中维特比译码具有最佳译码性能，但硬件实现相对复杂。veterbi算法是检测离散马儿可夫过程有限状态序列的优化算法。在数字通信系统中，前向纠错卷积码编码和维特比译码用来提高系统性能，应用广泛。

　　维特比算法是一种最大似然译码算法。它不是在网格图上一次比较所有可能的2条完整路径，而是接收一段，计算比较一段，选择一段最有可能的码段，从而达到整个码序列是一个有最大似然函数的序列。其基本原理是：以断续的接收码流为基础，逐个计算它与其他所有可能出现的连续的格状图路径的距离，选出其中概率最大的一条作为译码输出。

　　维特比(Veterbi)译码算法是基于卷积码的网格图表示中路径的计算，其核心思想就是通过计算路径矢量进而寻找最短路径从而最终得到译码序列并可以纠正传输过程中的错误码字。图4中给出(2，1，3)卷积码的网格图表示。

　　图4中的网格图中共有2k(N-1)种状态，每个状态(节点)有2k条支路进入，同时也有2k条支路引出。由于本文讨论的是(2，1，3)卷积码的情况，因此k=1，假设起始状态为全0。

　　在不同时刻对于同一节点的所有8个状态，分别计算以其为终点的2条分支路径的对数似然函数累加值并进行比较，舍弃其中对数似然函数累加值小的路径，保留对数似然函数累加值较大的路径，并将此路径称为剩余路径。由此可见，上述过程可以归纳为“加-比-选”算法，经过“加-比-选”电路以后，通过结束信息来确定最终得到的译码序列，其中每到来一个结束信息时，只将与已知发送信息相符的那条支路保留，以此类推，经过N-1个结束信息后，即可得到与发送序列最相似的译码路径。

　　3 译码器设计与实现

　　维特比译码器包括4个子模块，如图5所示。

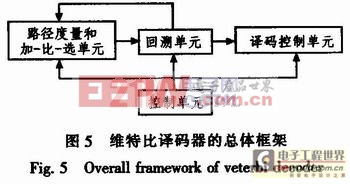
　　1)控制单元 向各个功能模块提供控制信号，保证译码器的工作时序正确，协调各个功能模块从而促使整个译码器的正常工作。

2)路径度量和“加-比-选单元”计算和比