AES算法中S-box和列混合单元的优化及FPGA实现

　　美国国家标准与技术局(National Institute of Standard and Technology，NIST)于1997年1月提出发展AES(Advanced Encryption Standard)加密算法，并于同年9月12日推出AES的早期基本算法。在研究了一系列早期算法之后，Rijndael算法被确定为先进加密标准(Advanced Encryption Standard，AES)。由于其较高的保密级别，AES算法被用来替代DES和3-DES，以适应更为严苛的数据加密需要。

　　与此同时，市场迫切需要AES的FPGA和ASIC的硬件解决方案，因为其与用软件实现相比更安全而且更省电。在一些应用，如：信用卡，手机，PDA等中，硬件的复杂度是影响成本和能耗的一个非常重要的因素。因此，在加密和解密中都非常需要优化AES的主要操作部分。在AES算法中，S-box是惟一的非线性单元，在加密解密，特别是字节替代和逆字节替代操作时需要分别执行S-box和逆S-box。建立一个16×16的S-box，以往通常采用查找表的方式实现，占用大量硬件资源。因此，对S-box进行优化是实现高效AES的重要步骤。

　　在此首先通过在S-box和逆S-box中共用一个look-up列表，简化非线性单元的复杂度，然后通过选择合适的即约多项式，进行域GF(28)到GF(24)的同构映射，对S-box的算法进行优化，并采用组合逻辑电路实现，使优化后的S-box在同等频率条件下较显著地减少了硬件资源的消耗。同时介绍了一种减小列混合(MixColumn)单元硬件复杂度的方案，可以明显地减少列混合单元的设计面积。

　　1 S-box的优化设计

　　在AES标准算法中定义了两个较大的列表。S-box和逆S-box。将S-box用于两个应用：字节替代和密钥扩展。而逆S-box则用于逆字节替代。这两个列表是不相同的，因此必须建立两个不同的ROM(256×8 b)，用以存储这两个列表。另外，在AES设计中使用平行结构，这就需要用到多个列表，这样会使硬件过于复杂，需要对其进行优化。以下主要对S-box模块进行结构优化。

　　1.1 S-box和逆S-box的组合

　　在一个高速128 b的AES设计中，一般需要总共20个S-box模块和16个逆S-box模块。其中，16个S-box模块用于实现字节替代的功能，4个S-box用于实现密钥扩展的功能，而16个逆S-box模块用于实现逆字节替代功能。在这种情形下，如果字节替代和逆字节替代时使用不同的列表，就会占用大量的硬件资源。所以非常需要一种减少硬件复杂性的方法。

　　就如AES标准所描述的那样，S-box的操作过程可以表示为：

　　因为multiplicative_inverse(乘法求逆)是一个相当复杂的方程，最常用的实现S-box的方法是运用look-up列表来由x得到y。等式(1)的逆等式如下：

　　因为multiplicative_inverse-1和multiplicative_inverse是相同的，所以等式(3)可以表述为：

　　最后，必须找到M-1，即矩阵M的有限域逆矩阵。由有限域逆矩阵的运算方法可知，可以计算出矩阵M的逆矩阵，命名为M’，如式(5)所示：

　　在式(1)和式(6)中，只使用了一个普通的look-up列表，从而将S-box和逆S-box集成，大大减少了字节替代和逆字节替代的硬件需求。图1展示了集成的S-box／逆S-box模块，可应用于AES的加密和解密。

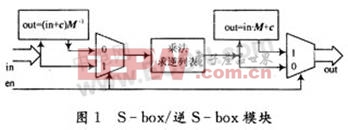
　　1.2 S-box单元中乘法求逆电路的优化

　　由第1.1节可知，S-box盒的生成电路由加密仿射电路(实现out=(in+c)M-1等式功能)，解密仿射电路(实现out=in·M+c等式功能)以及乘法求逆电路三个模块组成。要减少组合逻辑的复杂度，需要对乘法求逆电路进行优化。下面说明求逆电路的优化过程。

　　S-box硬件实现时的主要部件是乘法求逆。在有限域GF(28)上，乘法求逆是一种相当复杂的函数，直接在域GF(28)上生成S-box盒，组合逻辑复杂度高，会使电路中逻辑电路的门数大大增加。根据有限域的性质，利用域GF(28)与GF[(24)2]的同构变换，把GF(28)上的求逆转化在GF[(24)2]上的求逆运算，从而生成S-box单元，可以降低逻辑关系运算的复杂度，优化S-box的面积。

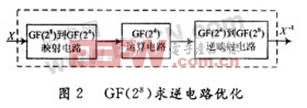
　　所采用有限域GF(28)上的乘法求逆电路模块优化过程如图2所示。优化的乘法求逆过程可表述如下：

　　(1)通过线性变换T将GF(28)的输入X映射到域GF(24)上的元素b，c；

　　(2)构建相应的域GF(24)的一次多项式，定义域GF(24)上的加法、乘法和求逆运算。利用域GF(24)上的加法、乘法和求逆运算，得到域GF(24)上元素b，c的逆元素p，q；

　　(3)构建线性变换T-1，将域GF(24)上的元素p，q映射到域GF(28)上，得到域GF(28)上的元素x的逆元素y=T-1(p，q)。

　　由有限域的知识可知，复合域GF[(24)2]中每个元素都可表示为系数在GF(24)上的一次多项式bx+c。设定义有限域GF[(24)2]的乘法的二次不可约多项式x2+Ax+B，可验证此时GF[(24)2]中的任一元素bx+c的乘逆元素是：

式中：(b2B+bcA+c2)-1是b2B+bcA