永磁同步调速系统自整定PI速度控制器设计

1 引言
永磁同步电机(PMSM)具有很多传统电机不具备的优势。它无电刷和滑环，转动惯量小，转矩脉动小，因而具有体积小，质量轻，功率损耗小等特点，并且随着电力电子技术和稀土永磁材料的快速发展，PMSM得到了广泛推广和应用。
对于PMSM的控制，目前应用最多的是双闭环控制且多采用PI调节器。经典的PI调节器工程设计法简单实用，但是会忽略很多因素，需要很多近似条件，并且在调节器参数不准确的情况下，所实现的控制效果往往不能达到预期要求，尤其是在给定值频繁变化的情况下。而模糊控制、神经网络控制等虽然能够通过增益自整定实现较好的控制效果，但又相对复杂、繁琐。
出于这种原因，这里采用了一种相对简单的增益自整定PI调节器的设计方法。利用此方法，基本可以实现类似于手工调节的过程，无需人为地对参数进行计算或整定。
为了验证理论分析的正确性及所采用的增益整定PI控制器的性能，这里利用Matlab进行了仿真，并且进行了相关实验。由仿真和实验结果可知，所提出的增益整定PI控制器的控制效果基本满足一般的控制要求。

2 原理与设计
2．1 永磁同步电机模型
2．1．1 永磁同步电机的数学模型
根据PMSM控制理论，正弦波PMSM一般没有阻尼绕组，转子磁通由永久磁钢决定，是恒定不变的，可采用转子磁链定向控制，即将两相旋转坐标系的d轴定在转子磁链ψr方向上，无需再采用任何计算磁链的模型。因此PMSM在d，q轴上的磁链方程简化为：
ψd=Lsdid+ψr，ψq=Lsqiq (1)
式中：id，iq为d，q轴电流；Lsd，Lsq为定子在d，q轴的电感。
d，q轴电压方程简化为：

式中：Rs为定子电阻；ωt为转速；p为微分算子。
转矩方程为：
Te=np(ψriq-ψqid) (3)
2．1．2 永磁同步电机双闭环控制系统模型
一个典型的磁场定向PMSM双闭环控制系统如图1所示。

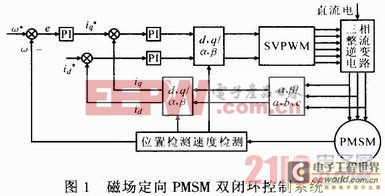
图中，内环为电流环，外环为速度环。速度环的给定ω*与检测出的电机实际转速ω的差值e作为PI速度调节器的给定，而速度环的输出又作为电流环的给定。定子电流作为反馈值经过坐标变换与电流给定值进行比较，差值作为PI电流调节器的给定值，而输出则控制逆变器的信号，从而调节电机的转速。这样就形成了双闭环控制系统。
2．2 增益整定PI速度控制器的设计
在PMSM双闭环控制系统中，电流环和速度环都采用PI控制器。
增益整定的PI控制器设计的基本思想就是当给定速度与实际速度相差很大，即差值很大时，增强比例环节的作用，增大比例增益，随着差值的减小，比例增益逐渐减小，积分的作用逐渐增强，并且当差值小于某一值时，积分作用达到最强，以减少静差。增益整定PI速度控制器的输出电压为：

图2示出增益整定PI速度控制器控制图。

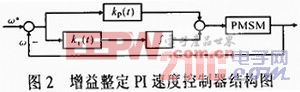
kp(t)的数学表达式为：
kp(t)=Kpmax-{Kpmax-Kpminexp[-(a|e(t)|)]} (5)
式中：Kpmax和Kpmin分别为比例增益的最大值和最小值；a为一个正常数，它决定了kp(t)在Kpmax与Kpmin间变化的快慢。
由式(5)可知，当e(t)非常大时，exp[-(a|e(t)|)]趋向于零，此时，kp(t)趋向于Kpmax；反之，当e(t)非常小时，exp[-(a|e(t)|)]将趋向于1，此时，kp(t)将趋向于Kpmin。ki(t)的数学表达式为：
ki(t)=[1-a(t)]Kimax (6)
式中：Kimax为ki(t)的最大值。
a(t)的范围是0～1，其表达式为：
a(t)=tanh[ηβ(t)] (7)
式中：η为一个正常数。
β(t)的表达式为：

因此a(t)的变化范围由0～1，且η决定了a(t)在0～1之间变化的快慢。
在过渡阶段，若要电机在很短的时间内达到期望的速度值，则需一个很大的控制信号。为了实现这一点，则需要一个很大的比例增益。由式(5)可知，当速度差值很大，即|e(t)|很大时，kp(t)能够得到保证，而由式(6)～式(9)可知，此时的ki(t)基本维持在最小。而随着电机转速的增加，速度差值逐渐减小，此时，kp(t)也随之减小。当实际速度到达期望值时，kp(t)变为零，以防止出现过大的超调，而ki(t)则到达最大值，并且基本直到稳态一直保持较大数值，以便消除稳态误差。

3 仿真和实验结果
3．1 仿真结果
通过Simulink进行仿真，可得到用增益整定PI速度控制器、PI电流控制器控制的PMSM双闭环控制系统的控制效果。电机参数：Rs=2．8 75 Ω，Ld=Lq=8．5 mH，ψ=0．175 Wb，J=0．093 kg·m2，np=4。增益整定PI速度控制器的参数：Kpmax=0．15，Kpmin=0．12，a=1，Kimax =0．009，η=5，ε=0．002。当速度给定为变化的值时，速度响应曲线如图3所示。

可知，第一次设定值为750 r·min-1，由零第一次到达750 r．min-1用时约0．032 s，并且从响应开始至到达稳态用时约0．1 s，超调量约为6．6％。在0．17 s左右设定值突变为400 r·min-1，在没有超调的情况下，用时约0．08 s响应达到稳态。在0．28 s左右给定值变为700 r·min-1，同样在没有超调的情况下，约用0．08 s响应到达稳态。就响应速度和超调量来看，基本满足一般的控制要求。

可知，在0．06 s处．当突加一个750 r·rain-1的速度时，给定与实际转速的差值相当大，因而kp(t)由最小值突增到最大值，然后继续保持在最大，而ki(t)则从最大骤然降为零，并保持在零处。在0．092 s左右，由于实际速度基本到达期望速度，因而，kp(t)由原来的最大值降为最小值，而ki(t)则由零突增到接近最大值，然后由于超调的产生，使得差值相对增大，因而积分作用再次减弱。比例放大作用再次增强。直至到达稳态时，kp(t)和ki(t)都趋向于一个适宜的稳态值，使系统继续保持稳定。在后面两个给定值发生变化的过程中，kp(t)与ki(t)的变化与第一个过程基本相同，在此不再赘述。由Matlab仿真的3个过程可知，比例与积分这两个增益的协调变化与预先设想的相同，并且能够使系统达到较满意的控制效果，从而验证了理论分析的正确性。
3．2 实验结果
结合上述理论分析和系统仿真，对理论进行了实验验证。图5a为速度不断变化时的速度响应曲线。可知，当期望值与起始值的差值较大时，kp(t)的作用很强，会产生足够小的超调量；而当差值较小时，则没有超调，并在约0．1 s内无静差地到达期望值。这与系统仿真的结果基本相符。图5b为速度在给定值为700 r·rain-1时的速度响应曲线。可知，从起始的100 r·min-1到达给定的700 r·rain-1，用时约为0．1 s，且只有很小的超调量。