基于FPGA的混沌加密虹膜识别系统设计

抑制功能。

实验表明，用不同的σ 高斯滤波器检测边缘，σ 越大，检测到的边缘越少，这一点可用滤波器的频率特性说明：

由于高斯函数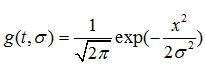的傅立叶变换为：

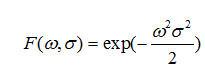（7-16）

可见高斯平滑滤波器为低通滤波器，但σ 越大，频带越窄，对较高频率的噪声有很强的噪声抑制作用。

为了可靠地检测边缘，有人同时用多个大小不同的尺度σ来进行滤波，这一点后来发展成为尺度滤波法。

7.3.3 利用边缘检测结果对图像进行二值化

对于灰度值没有变化的背景图像，其一阶二阶导数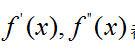都为零，灰度值递增，一阶导数大于零，灰度值递减，一阶导数小于零。对于图像的边缘，往往是图像灰度值激变的地方，其灰度的变化量达到峰值，即一阶导数达到极值点，相对应二阶导数为零，由数学分析中的函数理论可知，二阶导数为正的点其灰度曲线是凹的，而二阶导数为负的点其灰度曲线是凸的。对一幅灰度图像来讲，一旦灰度值发生变化，就可以从其二阶导数上反映出来，二 阶导数的正负可以反映灰度变化的形式。图10显示了一个函数及其二阶导数的图形。

设图9为图形中某一斑点的灰度截面图，则按照下式就可以使图像二值化，由背景图案中显示出此斑点。

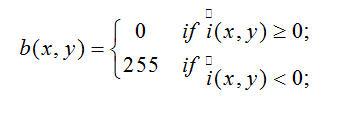（7-17）

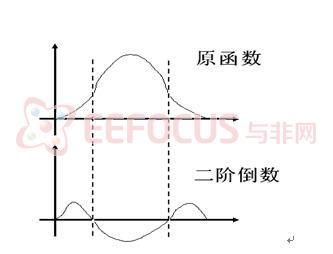
图10 函数及其二阶导数

式中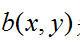为二值化的图像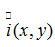，为由（7－14）式进行高斯拉普拉斯变换后的图像值，但是对于图像截面的斑点，二值化后的图像中却显示为一个圆环。对此，本文对式(7－17)做如下修正,以确保该点是一个斑点而不是一个圆环：若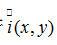大于等于零，则考察与它最近的非零点，若该点大于0，则其等于零，若该点小于零，则其等于255。在对图像的扫描中，实际上是从左到右进行的，一种简化的方法就是考察该已扫描的各点，由这些点中离该点最近的非零值来决定该点的值。因此二值化的表达式是：

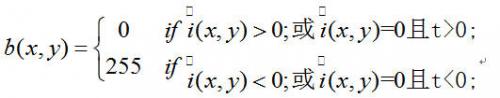
其中t 为图像中（x，y）前方的最近的一个非零点，这样改进以后可以减少特征点内部夹杂的斑点。

7.4 虹膜图像比对及识别理论分析

有上述陈述我们知，归一化后的虹膜图像大小为720*50，这使得前期计算量较大。提取出720*50位的二值编码后，在匹配时，用汉明距离(HD)对两个虹膜特征码进行匹配比对，公式如下：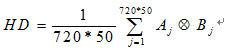

其中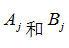，分别表示虹膜特征码A和B的第j位编码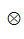，表示“异或”运算，当A和B对应的码字相同时(都是1或者0)，则异或值为0；A和B对应的码字不同时，则异或值为1。上式对两个长度为720*50位的虹膜码的对应每一位进行异或运算，如果两个虹膜码的每一位都相同，则HD=0；如果两个虹膜码的每一位都不同，则HD=1。因此，对于来自同一个虹膜的两幅图像来说，汉明距离比较小，对于来自不同虹膜的两幅图像来说，汉明距离比较大。

实际操作时，由于噪声影响以及前面处理过程中不可避免地会引入误差，来自于同一个虹膜的两幅图像的汉明距离不会是0，而是一个比较小的值；由于不同虹膜编码的对应位相等和不等的概率是一样的，因此，不同虹膜的两幅图像的汉明距离也不会是1，而是一个比较大的值。所以在匹配决策时，需要设定一个阈值，小于此阈值的两幅图像则认为属于同一个虹膜，反之，则认为属于不同的虹膜。

8.预期功能与目标

1）采集并识别虹膜图像，实现身份认证。

2）在无按键唤醒的状态下，系统暂停工作。

3）在工作状态下，通过在PC上的实时展示图像，进一步提高虹膜图像的获取质量。

4）在获取分辨率的虹膜图像的前提下，实现高精度的识别，将误差降到最低。

5）在TFT上精确显示比对结果，使得比对身份识别更加直观。