Canny算法的改进及FPGA实现

Canny边缘检测算法具有良好的信噪比和检测精度，因此在图像处理领域被广泛采用。但由于其计算量巨大，实时性较差，而且软件处理的设备体积较大，所以不适合实时检测。本文对原始Canny算法进行了分析、改进，并在FPGA中实现。实验证明新算法能满足实时性要求，而且检测精度和抗噪能力也较理想。

1 Canny边缘检测算法的基本原理

1.1 平滑图像

Canny边缘检测算法是高斯函数的一阶导数，是对信噪比与定位精度之乘积的最优化逼近算子。Canny算法首先用二维高斯函数的一阶导数对图像进行平滑[1]。设二维高斯函数为：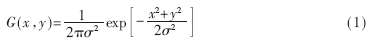

其梯度矢量为：

用分解的方法提高速度，把ΔG的2个滤波卷积模板分解为2个一维的行列滤波器：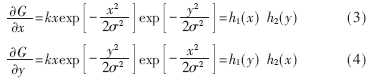

其中，k为常数，σ为高斯滤波器参数，它控制着平滑程度。对于σ小的滤波器，虽然定位精度高，但信噪比低；σ大的情况则相反。因此要根据需要适当地选取高斯滤波器参数σ。

1.2 计算梯度的幅值和方向

传统Canny算法采用2×2邻域一阶偏导的有限差分来计算平滑后的数据阵列I(x，y)的梯度幅值和梯度方向。其中，x和y方向偏导数的2个阵列Px[i，j]和Py[i，j]分别为：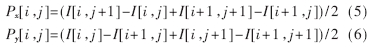

像素的梯度幅值和梯度方向用直角坐标到极坐标的坐标转化公式计算，用二阶范数来计算梯度幅值为：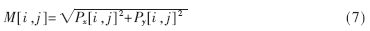

梯度方向为：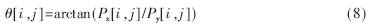


1.3 对梯度幅值进行非极大值抑制

为了精确定位边缘，必须细化梯度幅值图像M[i，j]中的屋脊带，只保留幅值局部变化最大的点，这一过程就是非极大值抑制。在非极大值抑制过程中，Canny算法使用3×3大小，包含8方向的邻域对梯度幅值阵列M[i，j]的所有像素沿梯度方向进行梯度幅值的插值。在每一个点上，邻域的中心像素m[i，j]与沿梯度方向的2个梯度幅值的插值结果进行比较。ζ[i，j]是像素邻域中心处沿着梯度方向的扇形区域，非极大值抑制在此区域进行。如果邻域中心点的幅值m[i，j]不比梯度方向上的2个插值结果大，则将m[i，j]对应的边缘标志位赋值为0，这一过程把M[i，j]宽屋脊带细化为一个像素宽，并且保留了屋脊的梯度幅值。非极大值抑制NMS(non-maxima suppression)过程的数学表示为：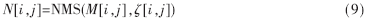


1.4 检测和连接边缘

双阈值算法是对经过非极大值抑制图像N[i，j]分别使用高、低2个阈值th和tl分割，得到2个阈值边缘图像Th[i，j]和Tl[i，j]。由于图像Th[i，j]是由高阈值得到，因此它应该不含有假边缘，但Th[i，j]可能在轮廓上有间断。因此双阈值算法要在Th[i，j]中把边缘连接成轮廓，当达到轮廓端点时，该算法就在由低阈值得到的边缘图像Tl[i，j]的8邻域位置寻找可以连接到轮廓上的边缘。这样，利用递归跟踪的算法不断地在Tl[i，j]中搜集边缘，直到将Th[i，j]中所有的间隙都连接起来为止。

2 算法的改进

传统Canny算子在2×2的邻域内求有限差分均值来计算梯度幅值的算法[2]，对边缘的定位比较准确，但对噪声过于敏感，容易检测出假边缘和丢失一些真实边缘的细节部分。针对传统Canny算法在梯度幅值计算上的缺陷，提出了一种在像素8邻域内通过计算x方向、y方向、135°方向、45°方向一阶偏导数有限差分来确定像素梯度幅值的方法。这种方法兼顾了梯度幅值计算中，边缘定位准确和抑制噪声的要求，在试验中取得了很好的效果。具体算法如下：

像素的梯度幅值和梯度方向用直角坐标到极坐标的坐标转化公式来计算，用二阶范数来计算梯度幅值为：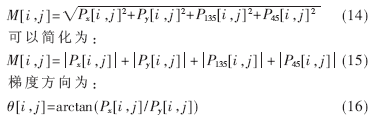

另外，传统算法中的边缘连接采取的是递归方法，不适合硬件实现，因此本文只进行了一次连接。其他改进具体体现在硬件实现的过程中，如用模板代替卷积， 加减法代替小数乘除等。

3 改进算法及FPGA实现

根据以上的数学推导及分析，得到Canny 边缘检测用FPGA实现的流程图，如图1所示。


3.1 高斯滤波

根据具体情况选择适当的σ，为了便于硬件实现可以采用模板来代替卷积运算。本文选择图2所示的模板，其中的乘除法系数都是2n的形式，因此可以用移位的方式实现，这避免了乘除法运算带来的时间与资源的消耗。计算中多次用到中心点的8邻域的值，因此设计了窗口形成模块，以便同时得到某个像素点的8邻域的值。原理图如图3所示。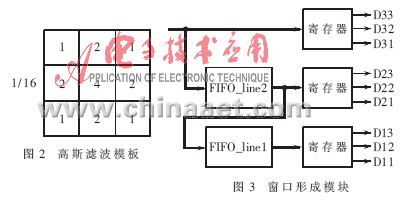

行延迟和列延迟分别由FIFO和寄存器完成，其中FIFO的深度等于图像的列数。

3.2 梯度计算

经过高斯滤波模块的数据再通过窗口形成模块，得到3×3邻域，然后按照式15，计算梯度的幅值。

梯度方向计算：根据8连通区域，量化边缘方向。首先将梯度角度的变化范围减小到圆周的1/8扇区。如图4所示，以0°、45°、90°、135°等为中心角度：每个方向包含±22.5°，根据Px Py的比值及正负确定其所在