小波变换在液氮制冷式露点自动检测中的应用

　　1　引言

　　冷凝式光学露点仪的制冷方式主要有半导体制冷和液氮制冷两种。用半导体制冷要使露点温度达到-60℃(绝对湿度为10·68×10-6)以下将会大幅度增加半导体器件制造工艺的复杂性,且不易实现;和半导体制冷相比,液氮制冷成本低,且容易实现。由于液氮制冷式露点仪受到检测光路系统灵敏度、降温速度、气体流量等因素的影响,使露点检测的稳定性不易掌握,因此露点测量值的重复性及准确度不甚理想。文献[1]指出,采用软件补偿方法可提高露点检测的稳定性。一般来说,在露点检测中欲达到较小的标准偏差(小于0·5℃),必须至少进行七次以上的测量,若进一步增加测量次数,虽可提高露点测量值的准确度,但将大大增加液氮的消耗,在实际露点测量操作中是不可取的。所以,提高液氮制冷式露点仪的检测准确度需要以更好的软件手段来实现。

　　2　露点测量不稳定现象分析

　　图1(a)为按某次实验中存储在计算机RAM中的一组测量数据绘制成的曲线。由图1(a)可见,用实测数据直接绘制的曲线为不光滑曲线,其中叠加有干扰噪声。为了改善曲线形状通常采用“五点三次平滑法”[2],这样得到的曲线如图1(b)所示。其中曲线Ⅰ为经平滑因子h(t)平滑后的情况,这实质上是对曲线的低通滤波,高频成分被削弱,但由于还存在着低频干扰,使平滑效果不够理想。其中曲线Ⅱ为经改变平滑因子h(t)的值可达到的效果,曲线平滑,但数据的真实性变差。由此可见,在软件处理上,已不可避免地存在着一定的偏差,并影响所求拐点数值的准确性。

　　3　小波变换的应用

　　3·1　小波变换的特征

　　小波变换是近几年新兴的一种先进分析方法,它被认为是傅里叶分析方法的突破性进展。小波变换是一种线性变换,它将信号分解成不同幅度(分辨率)的分量。假设ψ(t)是给定空间L2(R)内的实值或复值函数,且仅当以下方程成立时,函数ψ(t)被看成小波

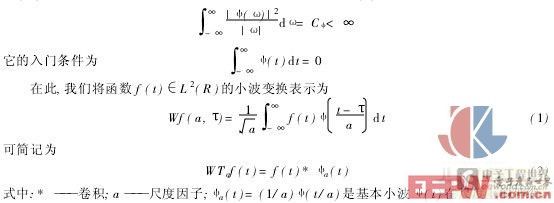
　　由式(1)可见,小波变换取决于两个参数:尺度a和时间位置τ。对于比较小的a值,小波集中于时间域,小波变换给出信号的细节信息;当a值较大时,小波扩展,小波变换给出信号的宏观信息。所以,运用小波变换的这种尺度可变性既能达到有效滤除噪声又能保证信号高保真度的目的。

　　3·2　利用小波变换处理测量信号的基本原理

　　如图1(a)所示,曲线基本上由A段较平坦部分与B段陡峭部分组成。曲线的拐点(t0,u0)可通过对函数f(t)求导获得,但求导运算会起放大噪声的作用,因而在噪声较大的场合,这种方法的效果并不理想。所以,引入小波变换技术以解决这一矛盾。

　　3·2·1　利用小波变换可有效抑制噪声

　　设{ Vj}是一给定在空间L2(R)中的闭子空间Vj的序列[3],并且所有的子空间Vj用同一个φ生成,即

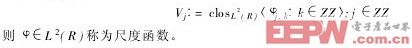
　　将上述关系表示为图2中的多采样滤波器组,图中H(ω)、G(ω)分别为低带通滤波器,由hn、gn经离散傅里叶变换取得

　　显然,在精细尺度上,由于信噪比小,要做的工作主要是极大地消去这些噪声,同时又能尽量保留原始数据结构信息;相反,在大的尺度上,由于信噪比大,数据结构的相关性较强,也可不做噪声滤波处理,以尽量多地保留原始数据。小波变换的这种类似于自适应的噪声处理方法,在曲线平滑处理中,可有效控制噪声而保证高的保真度。

　　3·2·2　曲线拐点的获取

　　设θ(t)为平滑函数,满足

　　所以,随着尺度a的增大,E[WTaf′(t)]2趋于零。即平稳噪声的小波变换均值为零,方差随尺度a增大而趋于零。并由此得出:平稳噪声的小波变换极值随尺度的增大而迅速衰减,而测量有效信号边沿对应的小波变换的极值随尺度的增大将增大(或稳定衰减)[4],从而成功地将有用信号的边沿与噪声加以区分。

　　4　主要算法的实现及实验结果

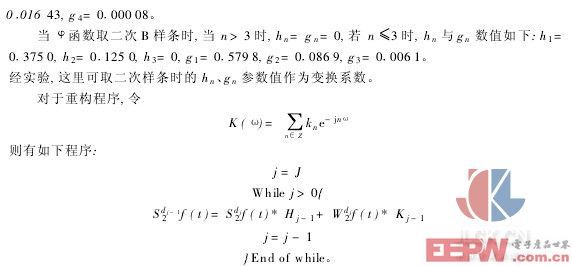
　　对于拐点的求取,首先由式(6)可获得WTaf(t),又可求得|WTaf(t)|的极大值,得f(t)的极值点,并确定曲线f(t)的拐点,同时,用Lipschits指数α来验算获取的极值,将信号在极值点t0处的Lipschits指数α与阈值α1比较,若α>α1,则认为信号在t0处发生了突变,α1的理论值为0[4]。在实际运用中,为补偿因软件运算过程中的误差,根据实验,取Lipschits指数α=-0·05,当a=2j,(j=3),取Δt为0·05 s,N=512时,经八次迭代,即可获得图3所示平滑逼近曲线及拐点值(t0,u0)。u0经换算可求得露点测量值。实验结果数据如表1所示。表2为传统方法所得露点值。其中

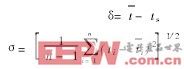
　　5　结束语

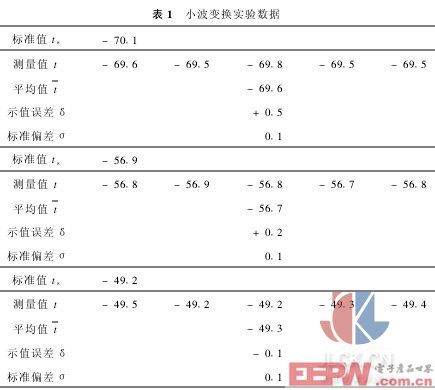
由于传统的数学处理方法虽然抑制了噪声,同时却极大地增宽了特征结构,因此存在计算值偏离真值的可能性,而小波变换方法除能很好地抑制干扰外,还尽可能多地保留原始信号的目标特征,从而可得到重复性及准确度更好的曲线和露点值,这点可由表1和表2的比较看出,其中用小波变换所得露点值的标准偏差小于0·1℃,测量平均值和示值的偏差在±0·5℃之内。另外,表中低湿