基于变结构混沌的伪随机序列发生器

式(5)～式(9)描述了混沌伪随机序列发生器设计的核心算法。实现一个混沌伪随机序列发生器可借助于软件和硬件平台。如果为计算机或其他软件提供伪随机序列，可借助数字计算机这个性能完善的平台实现式(5)～式(9)的运算，如可用Matlab，C语言等软件实现一个混沌伪随机序列发生器。也可结合实际应用在相关信号处理软硬件平台上实现混沌伪随机序列发生器，如利用DSP芯片对语音或视频信号进行混沌加密，可在DSP内进行上述运算而实现混沌伪随机序列发生器，也可利用FPGA硬件平台实现这种伪随机序列发生器。本文不侧重利用何种平台，如何实现混沌伪随机序列发生器，而是着重基于上述变结构混沌系统的伪随机序列发生器性能的测试。为此，选择Matlab求解变结构混沌系统，通过实现式(5)～式(9)的运算产生一系列伪随机序列，提取序列并进行序列的随机性统计测试。
描述一个序列随机性统计性能的指标有多种，但目前应用最广的是NIST(National Institute of Standardsand Technology，美国国家技术与标准局)标准。NIST推出2．0版本的测试软件包STS是当前最具权威的一种随机性检测工具，它为研究人员提供了一种量化的报告，显式地说明一个伪随机序列性能的好坏。STS-2．0b是当前最新的软件包版本，由十五项核心测试指标组成。
该测试包评价序列性能好坏有两项指标：其一是通过率，另一项是P-value分布的均匀性。测试独立生成的m组随机序列，依据各组每次测试的P-value值是否大于测试水平α=0．01来计算通过率。若各次测试的通过率在可信性区间内，其中1-a，则可说明此次测试算法的信任度高。对于P-value分布均匀性，若P-valueT>0．000 1，则说明P-value值是均匀分布的。
在Linux操作系统环境下进行测试。通过编程将变结构混沌系统进行离散迭代运算来产生数字混沌序列，然后将产生的二进制数字序列保存为txt文档，并通过测试指令调用软件包对txt文档中的序列进行测试，测试由STS软件包自动完成，并生成测试报告。基于变结构混沌系统产生的伪随机序列的测试结果如表1所示，序列共有100000000 b，以每组100000 b分为1 000组。

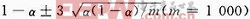从表1中P-value这一列看出，序列仅在FFT这一项中的P-value值测试不满足P-valueT>0．000 1的条件，这说明序列在该项测试中的P-value值分布不均匀，在其余14项测试中表现为分布均匀。若从通过率来分析，取显著水平α=0．01，那么根据通过率可信区间的计算公式可得，当PROPORTION的值落在(0．980 560 8，0．999 439 2)区间内时，表明序列通过该测试项，反之则为不通过。表1测试结果显示序列在所有测试中其结果均落在可信区间之内，所有指标均通过该项测试。

3 结论
为产生性能良好的伪随机序列，本文构造了一个新的变结构混沌系统。该系统在一个开关函数控制下自动地在两个混沌子系统之间随时问随机地转换，所产生的混沌信号是两个不同的混沌信号的混合，因而具有较好的复杂性。利用该变结构混沌系统设计了一种伪随机序列发生器，基于NIST标准和STS-2．0b测试套件对其产生的伪随机序列进行了测试，序列通过率全部通过了测试，序列的均匀性只有一项未通过测试。测试结果表明，该伪随机序列发生器具有良好的随机性能，可应用于计算机、通信、信息加密等领域之中。