基于变结构混沌的伪随机序列发生器

摘要：为产生随机性能良好的伪随机序列，提出了一个新的变结构混沌系统。该混沌系统在一个开关函数控制下其系统结构随时间随机地转换，所产生的混沌信号是两个不同的混沌信号的混合，具有良好的复杂性。基于该变结构混沌系统设计了一种伪随机序列发生器，采用NIST标准和STS-2．0b测试套件对其产生的伪随机序列进行了统计性能测试，测试结果表明该伪随机序列发生器具有良好的随机性，可应用于计算机、通信、信息加密等领域中。
关键词：混沌；变结构混沌；伪随机序列；随机性

0 引言
伪随机序列在数字通信、密码系统、计算机仿真等领域有着广泛的应用。一个伪随机序列发生器包括随机信号源(种)和一系列的离散、量化及其实现技术，其中良好的随机信号源是伪随机序列设计的关键问题。混沌与传统密码学之间存住着一种自然的联系，混沌动力学特性基本对应着高强度密码系统的某些安全特征，而具有良好混合特性的传统密码又蕴涵着混沌现象。以混沌作为信号源为伪随机序列发生器的设计提供了一种新的途径。
利用连续和离散混沌系统进行伪随机序列发生器的设计已有研究。离散混沌由于算法简单致使其运算速率快，序列码率较高，但缺点是系统参数和初值条件在一般情况下较少，密钥空间小，序列的安全性较低。连续混沌一股情况下是几个非线性微分方程的耦合，其系统参数和初始条件较多，产生伪随机序列的密钥空间较大，缺点是运算复杂，在数字系统实现时运算速率相对较慢。但如果采取合理的量化方法，会较好地弥补这种慢的运算速率。如在抽位量化方法中，如果一次抽取混沌数字迭代值的多位作为0，1序列，可大大提高其码率。因此采用复杂的连续混沌系统作为伪随机序列的源将是混沌序列应用的一个方向。
另一方面，数字系统的编码理论表明，在数字系统中处理非周期的混沌时，由于系统本身的有限位数致使混沌出现周期现象，即短周期或动力学退化问题。为改善这种短周期问题，可通过对混沌系统的变量或参数进行扰动以提高其数字PN序列的统计性能，增大序列的周期。为了提高混沌伪随机序列的复杂性和改善其动力性退化问题，本文设计了一个变结构混沌系统，以期获得性能更好的伪随机序列。所谓变结构混沌系统，是指该系统的代数结构不断地自动变化，而实现这种变化的控制函数是一个开关函数，该函数在自身变量控制下自动地在0，1之间转换。在提出变结构混沌系统之后，对基于该混沌系统的伪随机序列发生器进行了设计，对产生的伪随机序列进行了NIST(National Ins titute of Standards and Technology)测试。测试结果验证了该数字序列具有良好的随机性能。

1 变结构混沌系统构造
首先构造了一个三维连续混沌系统：

式中：a，b，c为可变的系统参数。在Matlab软件平台上计算表明，在较大的a，b，c参数范围内系统(1)都是混沌的，取a=0．8，b=1．5和c=1．5时系统(1)的时域波形和y-z平面上的轨迹(相图)如图1所示。

又构造了另一个三维连续混沌系统：

式中：a，b，c和是为可变的系统参数。在Matlab软件平台上计算表明，在较大的a，b，c和k参数范围内系统(2)都是混沌的，取a=0．8 b=1．5，c=1．5和k=0．32时系统(2)的时域波形和y-z平面上的轨迹(相图)如图2所示。比较图1和图2发现，两者的时域波形和对应的平面轨迹不同。

混沌系统(1)、(2)除第一个方程不同外，其余两个方程完全相同。虽然它们有相似的结构，但其代数结构不同，平衡点也不同(见下一节)，因而它们是非拓扑等价的，即它们在理论上是不同的两个系统。根据两个系统有相似结构但本质不同的特点，采用一个开关控制函数u构造了一个变结构混沌系统：

式中：m为开关控制函数的门限，m∈x取m=0．2，其他参数同前。对变结构混沌系统(3)进行仿真计算，所获得的时域波形x-t和y-z平面上的轨迹如图3所示。

图3中，实线和虚线分别为为系统(1)和(2)的波形或轨迹。
从图3看出，该系统的信号波形或解的轨迹由两个不同的部分构成。当系统的解x≥m=0．2时，u(x-m)=1，混沌系统(3)为混沌系统(2)的结构；当系统的解xm=0．2时，u(x-m)=0，式(3)变为混沌系统(1)的结构，如此往复变化。虽然在这种结构变化中的门限为一确定值，但由于混沌的不可预测性导致何时达到这一门限足无法预知的，即这种结构随时间而变化的规律是无法预知的，也是随机的。
这种由两个不同的混沌信号按时间随机地混杂在一起而形成的一个完整的混沌信号，比之由单一混沌系统产牛的信号要复杂得多，且门限参数本身又是一种密钥参数，它扩展了混沌伪随机序列的密钥空间，使其提高了安全性。

2 伪随机序列发生器设计及性能分析
基于上述的变结构混沌系统可设计一种新的伪随机序列发牛器。主要思路是以变结构混沌系统作为随机信号源，采用一定的方法对其离散、量化，获得一系列的伪随饥序列。
这里研究的变结构混沌系统是一个非线性常微分方程组，在数字系统中对其进行数值解就是一种离散的方法。常微分方程近似求解的数值方法有欧拉算法、改进型的欧拉算法和龙格库塔法等，这都是将连续系统进行近似离散化的方法。其中，欧拉算法速率最快，本文采用欧拉算法将连续混沌离散化。对于一个连续的混沌系统，有：


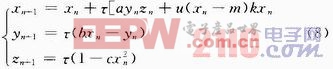
当τ足够小时，经过欧拉算法离散化后的系统具有与式(3)所示的连续混沌系统相同的动力学特性，此处选择τ=0．004。
在数字系统中迭代求解式(8)所示的离散化系统，迭代过程中的每一个解变量xn，yn和zn都可以通过二进制数据的方式来表示。以xn为例：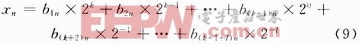

式中：b1n，b2n，…，b(k+1+l)n分别为二进制数的所有位(0或1)，混沌系统的解xn随时间不断变化，其二进制表达式中的每一位bm(“0”或“1”)也随时间小断变化。如果抽取随时间变化的一位或多位，可构成一个由“0”或“1”组成的伪随机序列。为了保证提取的序列具有较好的随机性，可以严格地从小数部分中提取其中一位作为随机序列，也可以从{b1n，b2n，…，b(k+1+l)n}中选取随机性能较好的多位作为随机序列，从而增加随机序列的提取速度。这种量化方法可用图4表示。