频差对方向图综合的影响及解决方法

摘 要：为解决各调频发射机开机时载波频差对天线阵列方向图综合的影响，这里利用了DFT 最大值谱线及与其相邻两根谱线系数的实部（或虚部）进行插值得到各个发射机载波频率的估算值，然后提出了一种有效的补偿方法，以减少频差引起的瞬时相位差对方向图综合的影响。仿真实验表明：此方法频率估算精度较高，采用该方法可以有效的解决频差对天线阵列方向图综合的影响。

0 引言

在通信条件恶化，环境、地形等不利于通信时，可以考虑利用智能天线技术将多部发射机组成一个天线阵列并机工作，与单部发射机相比，发射功率更大，方向性更强，更加有利于通信。现研究对发射机载波频差对天线方向图的影响进行了仿真分析，而后利用DFT 最大值谱线及与其相邻两根谱线系数的实部（或虚部）进行插值得到频率估计值，然后采用数字振荡器进行频偏校正，并且通过MATLAB/ SIMULINK仿真实验验证了这种方法是可行的，取得了较好的效果。

1 实验原理

1.1 系统框图

这里实验系统是利用智能天线技术将多部调频发射机组合成一个均匀直线阵列，以期在通信条件恶化时保证通信正常进行。但是在发射机开机之后，各发射机载波频率会有所不同，这样会对合成后的天线方向图产生严重的影响，进而影响通信能力的增强。为此，提出了首先对各个载频进行精确估计，然后利用数字振荡器对频率进行校正，使各发射机调频输出信号载频相同，以获得较好的方向图。仿真实验系统框图如图1 所示。

图1 简单仿真实验系统

　　该实验需用5 部调频发射机组成一个均匀直线阵列，以第一部发射机的调频输出信号的载频为参考，利用离散傅里叶变换（DFT，Discrete Fourier Transform），最大值谱线及与其相邻两根谱线系数的实部（或虚部）进行插值得到频率估计值，然后进行频率校正直至各调频输出信号载频基本相同。其中，参考信号的获取是通过在天线底端加一个耦合器及其匹配电路，然后将信号引入频率估计端口进行数值运算。

1.2 直线阵模型

该研究将各发射机天线组成一均匀直线阵列，这是一种最简单的阵列结构，所有阵元等间距排列在一条直线上。假设阵元的位置位于（xm, ym ），m =1,2,……,N ,以原点为参考点，α表示方位角（入射信号与y 轴的夹角，也就是与阵列法线的夹角），如图2 所示。图2 中d 为阵元间距（一般为入射信号波长的一半），以最左边的阵元为参考点，α 为入射到阵列上的平面波的方位角。

图2 均匀直线阵示意

则可以得到阵列的方向图为：

式（1）中：，为波数；d 为阵元间距；θ 0为方位角。

将各个调频发射机的输出信号作为阵元的激励，得到的方向图为：

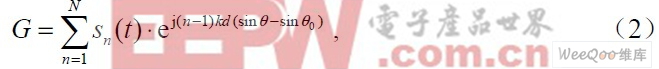
其中， sn（t） 是第n 路发射机输出信号，其表达式为：

这样会对方向图综合产生严重影响，因此，必须首先进行频率估计，而后进行相应的相位补偿，以减小对方向图的综合的影响。

1.3 基于FFT 的频率估计和频率校正

利用DFT 最大值谱线及与其相邻两根谱线系数的实部（或虚部）进行插值得到频率估计值。

设信号为正弦信号，表示为：

　　式（5）中：x（n）为未知离散实正弦信号， a, f0 ,φ 分别是信号的幅度、频率、和初相；f s为信号采样频率。

基于DFT 的谱分析方法，具有运算速度快（采用快速傅里叶变换（FFT，Fast Fourier Transform））、对正弦信号具有显着的信噪比增益和具有算法参数不敏感等优点，是一个综合性能最佳的方法，因此得到了广泛的应用。但是由于存在栅栏效应，当采样频率不是DFT 频率分辨率的整数倍时，正弦信号频谱发生泄漏，即使无噪声影响，信号真实频率仍落于主瓣内两根离散FFT 谱线之间，导致频率估计无法满足精度要求。因此，介绍一种插值方法，以提高频率估计的精确度。

x（n）的N 点离散时间信号的傅里叶变换（DFT）记为X（k），鉴于实序列DFT 的对称性，忽略频谱的负频率部分，即：

式（6）中T = N / fs 为采样的长度。

假设m k 是对应的X（k）取得最大值时的序号值，那么式（6）中f0T 可表示为km + δ ，δ∈[-0.5,0.5]，因而有：

当N 取较大值时，式（7）可表示为：

式（8）为一般情况下正弦波信号的DFT 系数表达式。

根据式（8）可以得到km谱线幅值为：

紧邻km的两条谱线（ km +1和km -1处）幅值近似为：

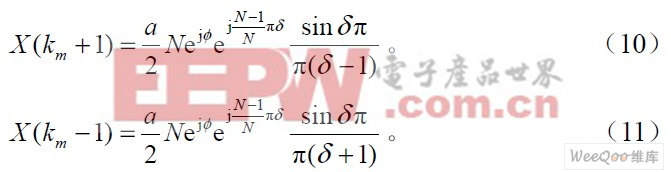
根据式（8）、式（9）和式（10）可以推导得到以下两式：

从式（9）、式（10）和式（11）中可以看到X （km）、X （km +1）和X （km -1） 实部和虚部的大小与角度φ + （（N -1） / N）πδ 相关联，当cos[φ + （（N-1） / N）πδ]比sin[φ+（（N -1）/N）