轻轻松松让你学会阻抗匹配原理和方法

阻抗匹配（Impedance matching）是微波电子学里的一部分，主要用于传输线上，来达至所有高频的微波信号皆能传至负载点的目的，几乎不会有信号反射回来源点，从而提升能源效益。

阻抗匹配有两种，一种是透过改变阻抗力（lumped-circuit matching），另一种则是调整传输线的波长（transmission line matching）。

要匹配一组线路，首先把负载点的阻抗值，除以传输线的特性阻抗值来归一化，然后把数值划在史密斯图上。

改变阻抗力
把电容或电感与负载串联起来，即可增加或减少负载的阻抗值，在图表上的点会沿着代表实数电阻的圆圈走动。如果把电容或电感接地，首先图表上的点会以图中心 旋转180度，然后才沿电阻圈走动，再沿中心旋转180度。重复以上方法直至电阻值变成1，即可直接把阻抗力变为零完成匹配。

阻抗匹配：简单的说就是「特性阻抗」等于「负载阻抗」。

调整传输线
由负载点至来源点加长传输线，在图表上的圆点会沿着图中心以逆时针方向走动，直至走到电阻值为1的圆圈上，即可加电容或电感把阻抗力调整为零，完成匹配。

　  阻抗匹配则传输功率大，对于一个电源来讲，单它的内阻等于负载时，输出功率最大，此时阻抗匹配。最大功率传输定理，如果是高频的话，就是无反射波。 对于普通的宽频放大器，输出阻抗50Ω，功率传输电路中需要考虑阻抗匹配，可是如果信号波长远远大于电缆长度，即缆长可以忽略的话，就无须考虑阻抗匹配 了。阻抗匹配是指在能量传输时,要求负载阻抗要和传输线的特征阻抗相等,此时的传输不会产生反射,这表明所有能量都被负载吸收了.反之则在传输中有能量损 失。高速PCB布线时，为了防止信号的反射，要求是线路的阻抗为50欧姆。这是个大约的数字,一般规定同轴电缆基带50欧姆,频带75欧姆,对绞线则为 100欧姆,只是取个整而已,为了匹配方便.

　　阻抗从字面上看就与电阻不一样，其中只有一个阻字是相同的，而另一个抗字呢？简单地说，阻抗就是电阻加电抗，所以才叫阻抗；周延一点地说，阻抗就是电 阻、电容抗及电感抗在向量上的和。在直流电的世界中，物体对电流阻碍的作用叫做电阻，世界上所有的物质都有电阻，只是电阻值的大小差异而已。电阻小的物质 称作良导体，电阻很大的物质称作非导体，而最近在高科技领域中称的超导体，则是一种电阻值几近于零的东西。但是在交流电的领域中则除了电阻会阻碍电流以 外，电容及电感也会阻碍电流的流动，这种作用就称之为电抗，意即抵抗电流的作用。电容及电感的电抗分别称作电容抗及电感抗，简称容抗及感抗。它们的计量单 位与电阻一样是欧姆，而其值的大小则和交流电的频率有关系，频率愈高则容抗愈小感抗愈大，频率愈低则容抗愈大而感抗愈小。此外电容抗和电感抗还有相位角度 的问题，具有向量上的关系式，因此才会说：阻抗是电阻与电抗在向量上的和。

　　阻抗匹配是指负载阻抗与激励源内部阻抗互相适配，得到最大功率输出的一种工作状态。对于不同特性的电路，匹配条件是不一样的。

　　在纯电阻电路中，当负载电阻等于激励源内阻时，则输出功率为最大，这种工作状态称为匹配，否则称为失配。

　　当激励源内阻抗和负载阻抗含有电抗成份时，为使负载得到最大功率，负载阻抗与内阻必须满足共扼关系，即电阻成份相等，电抗成份只数值相等而符号相反。这种匹配条件称为共扼匹配。

史密斯图(Smith chart)是一款用于电机与电子工程学的图表，主要用于传输线的阻抗匹配上。一条传输线 (transmission line)的阻抗(impedance)会随其物理长度而改变，要设计一套阻抗匹配(Impedance matching)的电路，需要通过不少繁复的计算程序，史密斯图的特点便是省却一些计算程序。

该图表是由菲利普•史密斯(Phillip Smith)于1939年发明的，当时他在美国的RCA公司工作。史密斯曾说过，「在我能够使用计算尺的时候，我对以图表方式来表达数学上的关联很有兴趣。」

史密斯图的基本在于以下的算式

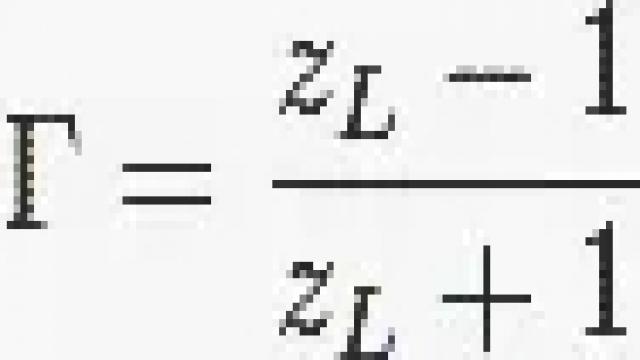
当中的Γ代表其线路的反射系数(reflection coefficient)，即S-parameter里的S11，zL是归一负载值，即ZL / Z0。当中，ZL是电路的负载值；Z0是传输线的特性阻抗值，通常会使用50Ω。

图表中的圆形线代表电阻抗力的实数值，即电阻值，中间的横线与向上和向下散出的线则代表电阻抗力的虚数值，即由电容或电感在高频下所产生的阻力，当中向上 的是正数，向下的是负数。图表最中间的点(1+j0)代表一个已匹配(matched)的电阻数值(ZL)，同时其反射系数的值会是零。图表的边缘代表其 反射系数的长度是1，即100%反射。在图边的数字代表反射系数的角度(0-180度)和波长(由零至半个波长)。

有一些图表是以导纳值(admittance)来表示，把上述的阻抗值版本旋转180度即可。

自从有了计算机后，此种图表的使用率随之而下，但仍常用来表示特定的资料。对于就读电磁学及微波电子学的学生来说，在解决课本问题仍然很实用，因此史密斯图至今仍是重要的教学用具。

在学术论文里，量度仪器的结果也常会以史密斯图来表示。