基于小波变换的图像压缩算法改进研究

摘要：本文首先分析了基于小波变换图像压缩原理、流程和方法，然后针对传统的嵌入式小波零树压缩编码算法的不足，提出了改进方案。改进方案包括使用正交小波基Z97替代小波变换，使用排除法减少对重要系数的扫描次数，使用多种扫描顺序替换单一的“Z”字型扫描等。仿真实验结果表明，改进的方案提高了图像压缩效率，改善了重构图像的质量。

引言

作为信息的重要载体，数字图像因具有直观、明确、高效、丰富等优点一直受到人们的欢迎。但是，随着多媒体和网络技术的快速发展和深入应用，海量的图像信息与有限的存储容量、有限的处理能力以及有限的网络带宽之间的矛盾日益突出。因此，图像压缩是必不可少的，同时，也已经成为了研究热点。研究主要集中在两个方向，一是通过减少各类冗余信息以实现图像压缩;二是根据图像数据分布情况及其出现频率，确定合适的编码方式，减少每个数据所占的比特数，从而实现图像压缩。作为第二代图像压缩编码方式，小波变换具有时频局部化、多尺度、多分辨率、能量聚集等优势，因而广泛应用于图像压缩领域。本文在分析传统的嵌入式小波零树压缩编码的基础上，分别针对小波变换阶段、零树构造阶段和扫描阶段提出了改进方案。仿真实验结果表明，改进的方案提高了图像压缩效率，改善了重构图像的质量。

1 小波变换

1.1 小波变换的产生及原理

尽管傅里叶(Fourier)变换可以确切地告诉人们某个信号是否包含特定的频率分量，但它无法说明该频率分量发生在哪个时间段。因此，它仅适用于处理平稳信号，而不适用于处理非平稳信号。如果将非平稳信号的某些局部区间看作平稳的，这个局部区间仍可以采用傅里叶变换，即短时傅里叶变换(SIFT)。SIFT包括了频率分辨率和时间分辨率，一定程度上克服了Fourier的缺陷，但是，SIFT提高时间分辨率要以牺牲频率分辨率为代价，反之亦然。SIFT的另一缺陷是无论如何离散化其变换核，都无法得到一组正交基，使其实用性大大降低。

小波变换弥补了SIFT的不足，它将原始信号通过伸缩和平移之后，分解成一系列具有不同空间分辨率、不同频率特性和不同方向特性的子带信号，这些具有良好时频特性的子带信号可以用来表示原始信号的局部特征，从而实现了对原始信号进行时间和频率上的局部化分析。因此，小波变换被广泛应用于图像分析、语音编码和模式识别等领域。

1.2 小波变换的定义

定义1：小波变换

假设函数，并且是紧支撑的，即，通过伸缩、平移母小波函数可得到分析小波：

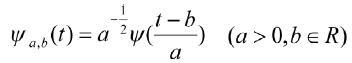(1)

其中，a和b分别是尺度参数和平移参数。可以通过改变a和b的值，实现调整分析小波的时频窗中心和时频窗长度的目标。实质上，小波变换是一种窗口形状可变，但面积不变的时频局部化分析工具。

定义2：连续小波变换

对于信号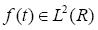，其连续小波变换为：

(2)

其逆变换为：

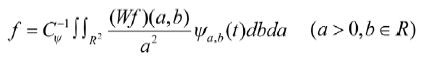(3)

其中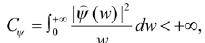，为小波系数(wf)(a,b)，其值越大，信号与小波越相似。

定义3：离散小波变换

为了减少冗余信息，降低计算量，将尺度参数a和平移参数b离散化，令a=a₀^-m，b=nb₀a₀^-m，a₀和b₀分别是固定的伸缩步长和平移步长，离散小波变换为：

(4)

2 基于小波变换的图像压缩

2.1 基于小波变换的图像压缩基本流程

小波图像压缩基本流程包括编码和解码两个阶段。编码阶段分为三步：首先，对图像进行小波变换，然后，对小波系数进行量化，最后，进行图像编码，生成压缩图像。解码阶段则包括相应的图像解码、小波系数反量化和小波逆变换，最后生成重构图像。基于小波变换的图像压缩流程如图1所示。

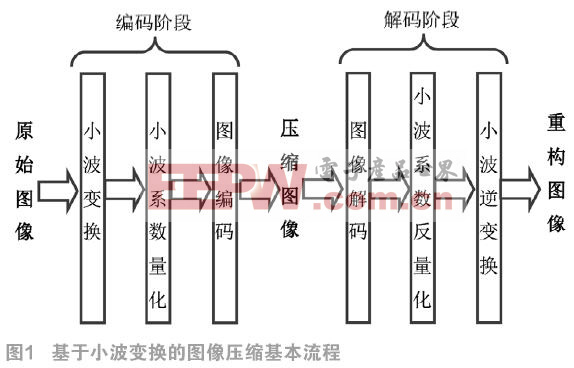
2.2 基于小波变换的图像压缩编码

基于小波变换的图像压缩能够实现较高的压缩比和比较理想的图像恢复质量，因此它成功地替代DCT成为了JPEG2000、MPEG-4和MPEG-7的编码标准。目前常用的小波图像编码分别是嵌入式小波零树图像编码(EZW)、分层小波树集合分割算法(SPIHT)和优化截断点的嵌入块编码算法(EBCOT)。EZW利用相同方向、不同分辨率子带图像间的相似性，定义POS、NEG、IZ和ZTR四种符号进行空间小波树递归编码，把不重要的小波系数组成四叉树，然后用较少的比特数表示，从而有效地提高了图像压缩率。SPIHT利用空间树分层分割方法，将某一树结点及其所有后继结点划归为同一集合，有效地减少了比特编码符号集的规模。EBCOT将子带划分为若干块，然后对每个块进行编码，产生压缩码流。

3 嵌入式小波零树压缩编码算法及改进方案

3.1 传统嵌入式小波零树压缩编码算法

嵌入式编码是指截取一段从起始位置开始，在任意位置结束的编码码流，可以进行解码重构整幅原始图像，截取的码流越长，重构的图像越接近原始图像。与原来的全部码流相