Harris角点提取实现亚像素级摄像机自标定

1 引言
基于单平面模板的摄像机自标定是当前应用比较广泛的摄像机标定方法，只需要摄像机从不同方向拍摄3幅用于标定的图像(棋盘格)，提取出其中的角点，根据其与平面模板间的关系，确定单应性矩阵，便可以计算出摄像机的全部内参数。其优点是操作简便并且无需知道模板的运动情况。但这种标定方法要求标定图像非常平整，而且要求角点清晰易分辨。无形中就约束了激光打印机的精度。而准确提取标定板上特征点的坐标是这种自标定中最为关键的一步，直接关系到标定结果的精确度。为解决这一问题，提出利用Harris算法提取出角点后，再将其坐标精确到亚像素级，以提高标定的精度。

2 基于Harris算法的角点提取
Harris算子是Harris和Stephens在1988年提出的一种基于静止图像的点特征提取算子。这种算子受信号处理中自相关函数的启发，给出与自相关函数相联系的矩阵。矩阵的特征值是自相关函数的一阶曲率，对图像中的任意一点，如果它的水平曲率和垂直曲率值都高于局部邻域中其他点，则认为该点是特征点。它计算简单有效同时非常稳定，在图像旋转、灰度、噪声影响和视点变换的条件下，与其他算子相比是最稳定的一种点特征提取算子。Harris算子定义为：

式中：其中gx为x方向的梯度，gy为y方向的梯度，G(s)为高斯模板，为卷积操作，I为每点的兴趣值；det为矩阵的行列式；tr为矩阵的迹；k为经验值，一般取0.04。
Harris算子在摄像机标定图像的使用方法：首先计算图像中的每个点在横向和纵向的一阶导数以及它们的乘积。从而得到3幅新的图像。这3幅图像中的每个像素对应的属性值分别为gx，gy和gxgy。然后运用高斯滤波处理这3幅图像，接着计算原图像上对应的每个点的兴趣值。计算完各点的兴趣值后，要提取出原始图像中的所有局部兴趣值最大的点，即依次取出每个像素的8邻域中的每个像素，从这些像素中找出兴趣值最大者。特征点就是中心点像素的兴趣值为最大的点。
用公式提取特征点时，只要像素点的兴趣值大于某一阈值T的点均可被认为是特征点。但T不具有直观的物理意义，其具体值难以确定。所以在实际操作中应采取间接确定T的方法：通过确定图像中所能提取的最大可能的特征点数目N来选择兴趣值最大的若干像素点作为特征点。局部极值点的数目可能会很多，根据兴趣值进行排序后，取其前N个点为特征点。

3 精确角点坐标至亚像素级
对于棋盘格图像如图1所示，角点附近的点可分为在边缘上的点和不在边缘上的点两类。B点上的梯度方向与OB垂直，而A点处灰度梯度为零，可见在角点O附近点的灰度梯度均垂直于该点与角点的连线。

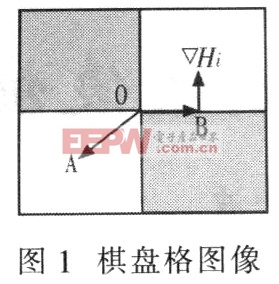
用数学式可表达如下：

式中：为灰度梯度向量，为图像原点指向O点的坐标，为图像原点指向第i点的坐标。
实际图像可能受到噪声的影响，故一般情况下式(1)不为0。设误差为θ，即：

在以角点为中心的某一邻域内，对所有点按式(2)计算，误差和为S，则有：

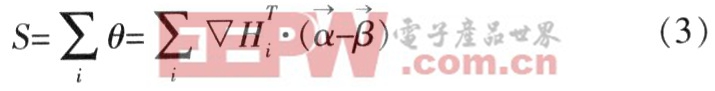
故求角点准确位置的问题转化为求使误差和S最小的点的问题。该问题可用迭代的方法优化求解，对式(1)两端同时乘以得：

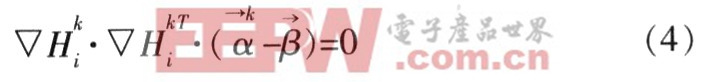
将角点邻域内所有点分别代入式(4)。把所有结果求和，可得出：

这样就得到了角点O的迭代式，通过对初始Harris角点进行一定级数的迭代优化，可以得到其更精确的坐标位置。

4 自标定算法
自标定算法采用张正友标定法，其大致过程如下：
(1)坐标系变换

由此式(8)可完成从摄像机坐标系到图像坐标系的变换，其中A包含摄像机的全部6个内参数,f为摄像机焦距，θ为摄像机坐标系的偏斜度，像素点的大小为k×l，单位为mm，图像坐标系的原点位于(u0,v0)上。
摄像机坐标系和世界坐标系的关系为：

式中：R3×3为旋转矩阵，t3×1为平移向量。
由式(7)和式(9)可得从世界坐标系到图像坐标系的一个线形变换：km3×1=A(R3×3，t3x1)M3×1，其中m3×1为图像点的齐次坐标，M3×1为三维空间点的齐次坐标，为比例系数。
(2)计算透视投影矩 令H=λA(R，t)，其中λ为比例系数，H为透视投影矩阵，可通过已知的一系列二维、三维点对获得，即将所有对应点对(角点)的Mahalanobis距离标函数，利用最大似然估计的方法获取当Mahalanobis距离取到最小值时的H矩阵。
(3)摄像机参数的获取设标定板放在世界坐标系的Z=0平面内，可得到只包含两个列向量的旋转矩阵，再由所选坐标系为笛卡儿坐标系，可得到关于矩阵A的两个约束条件，这样便可求出透视投影矩阵，再由式H=λA(R，t)，可得到摄像机的全部内参数。
(4)径向畸变的矫正 由畸变模型为：

式中：(x，y)原图像坐标，(x,y)为校正后图像坐标，k1，k2为径向畸变系数，由Levenberg-Marquardt算法实现非线性优化校正过程。