基于改进遗传算法的油田配电网无功优化

引言
随着油气田勘探与开发力度的不断加大．油气田内部用电负荷急剧增加，各油田采油成本中电耗已占到三分之一以上，因此在满足负荷用电需求的基础上，保证供电质量的同时，降低油气田电网网损，已成为油田电力系统急需研究解决的问题，而无功优化则是解决这一问题的重要手段。油田配电网普遍网损大、电压合格率低。资料表明：油气田13％的电能是在配电系统中消耗掉的，因此研究油气田配电网无功优化的实用性具有重要意义。
配电网无功优化是指在确定系统有功潮流分布情况下，优化调节某些控制变量，在满足系统各种约束条件的前提下使系统有功网损达到最小，这是一个多约束的非线性整数规划问题，其优化变量既有连续变量又有离散变量，使得整个优化过程非常复杂。多年以来，研究人员已提出了许多无功优化方法，如非线性规划法、线性规划法、动态规划法和混合整数法等，但是这些方法都普遍存在对初始解的特殊要求以及不便于处理离散变量等缺陷。油田配电网具有其自身的特点，比如线路的R／X比值较大；闭环设计、开环运行的的网络拓扑其呈辐射状分布；网络的PQ节点多，PV节点少，特别是优化过程中离散变量的处理更增加了优化难度。
遗传算法(Genetic Algorithm,简称GA)，又称基因算法，是一种模拟自然选择和遗传机制的随机优化算法，它只需目标函数作为寻优信息，通过对初始群体的不断选择、交叉、变异来找到最优个体，具有很强的全局寻优能力和处理离散变量特性。由于遗传算法在解决多变量、非线性、不连续、多约束的问题时显示出其独特优势，这使得该算法在无功优化领域中的应用倍受关注。但在实际研究中，传统遗传算法也暴露出诸如：收敛速度慢、易早熟等缺陷。针对这些问题，应用自适应遗传算法，并对传统遗传算法的遗传算子和终止判据等方面进行改进，提出了一种适合油田配电网无功优化的改进遗传算法。

2 无功优化问题数学模型
油气田配电网无功优化采用合适的电容补偿和调节变压器分接头等方法提高电压质量，降低损耗。用优化方法确定无功补偿容量、补偿地点、变压器分接头位置及其之间的相互配合。其数学模型包括潮流(功率)约束方程、变量约束方程和目标函数。以有功网损最小为目标函数，选择无功补偿源节点的注入无功及变压器的可调分接头作为控制变量。
2．1 目标函数
油气田配电网一般是由一个电源点(根节点)构成的辐射状网络，线路和节点较多，而PV节点很少甚至没有。因此，目标函数和约束条件可以不考虑发电机节点的无功调节和罚函数项，容性无功的上下限选取主要受投资和安装空间的限制。因此，对油气配电网的无功优化问题建立目标函数如下：

式中：ω1为有功网损年费用平衡系数；△P为系统有功损耗；τmax为年最大负荷损耗小时数；C为系统电价，元/kw?h；ω2为电压越界罚因子；ω3为电容器固定安装费用，万元/节点；nc为补偿电容器的个数；ω4为电容器年运行费用，万元／kvar；Qc为系统的电容补偿总容量：n为配电网节点数。式(1)的第一项为配电网年运行费用，第二项为电压越界罚项，第三和第四项为电容器年补偿费用。
在无功优化中，目标函数越小越好，而在遗传算法中，适应度越大越好。所以适应度函数采用目标函数的倒数：

f=1/F (2)
式中：f为适应度函数，F为目标函数。
2．2 等式约束条件
油田配电网无功优化的等式约束条件为节点潮流方程：

式中：Pi、Qi分别为节点i注入的有功功率和无功功率；Gij、Bij、θij分别为节点i与节点j之间的电导、电纳和节点电压相位差角：n为配电网节点数。
系统的有功损耗为：

式中：h为所有与节点j相连节点的集合。
2．3 不等式约束条件
控制变量不等式约束条件如下：

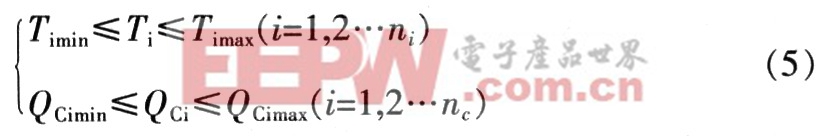
式中：Ti为分接头可调变压器的变比；Qci为补偿电容量，ni为有载调压变压器的台数。
状态变量不等式约束条件如下：

式中：Vi为节点i的电压；Qi为节点i注入的无功功率。

3 改进遗传算法
遗传算法是一种模拟自然选择和遗传机制的随机优化算法，它只需目标函数作为寻优信息，通过对初始群体的不断选择、交叉、变异来找到最优个体，因此具有很强的全局寻优能力和处理离散变量的特性。但传统遗传算法采用二进制编码方式，遗传算子采用轮盘赌、中一点杂交、中一点变异，存在收敛速度慢、易早熟等缺陷。由于油气田配电网节点多，线路长，这个缺点更加突出。针对此问题，这里应用自适应遗传算法，对常规遗传算法的编码方式、遗传算子、终止判据等方面进行改进，提出一种适合于油田配电网无功优化的改进遗传算法。使无功优化补偿计算得到的负荷电压水平、网络损耗均较常规遗传算法结果更优。
3．1 编码方式的改进
编码是应用遗传算法时要解决的首要问题，也是设计遗传算法的一个关键步骤。传统遗传算法采用二进制编码方式来建立解空间与染色体空间的一一对应关系。对于无功优化这样多变量的复杂优化问题，由于其控制变量维数很多，采用二进制编码方式，为了保证问题的解具有一定的精度，则其个体的编码串将很长，从而使遗传操作的计算量较大，计算时间增多，需要更多的内存空间，同时其搜索空间亦很大，导致搜索性能很差，收敛速度很慢。基于无功优化问题这样的特点，若采用浮点数编码方式，即个体的每个基因值用变量取值范围内的一个浮点数来表示，个体的编码长度等于其控制变量的个数。因此其个体染色体编码长度大大减小，极大地降低了其搜索空间，提高了收敛速度。
3．2 选择操作的改进
选择是最具有自然进行特色的操作之一，它是从所有母体中选取部分个体组成繁殖库的过程。作为交叉和变异的前提，选择过程应保证越优良的个体越有较大的几率被选中，而适应值低的个体渐渐被淘汰，即所谓的“优胜劣汰”。
选择操作是建立在对个体的适应度评价的基础之上，有时直接关系到收敛速度问题。采用两两竞争的选择策略，首先从群体中随机选取两个个体比较适应度，将其中适应度最高的个体遗传到下一代群体中；然后将上述过程重复M次，就可得到繁殖库所需的M个个体。
该种选择策略使每个个体入选繁殖库的概率与其适应值不直接成比例。所以它能使群体在解空间上有较好的分散性，使得个别大适应度值的个体在种群中不会出现大量繁殖的现象，同时又保证了加入繁殖库中的个体有较好的适应值。另外两两竞争选择策略对个体适应度是否取正值无特别要求，因此可直接用问题的目标函数当作适应度函数。
由于选择、交叉、变异等遗传操作的随机性，为了防止在进化过程中得到的最优个体被其破坏，采取保存最优个体策略，即当前群体中适应度最高的个体不参与交叉和变异运算而直接进入下一代，该策略的实施保证算法的收敛。
3．3 交叉和变异算子的改进
交叉是遗传算法中寻找最优个体的最主要手段，也是遗传算法区别于其他优化方法的主要标志。变异是避免“近亲繁殖”，保持群体多样性，实现多路径搜索，以避免局部收敛，恢复丢失的或寻找尚未得到的优良信息的主要工具，它是以较小的概率使密码串中的某码位产生突变。
传统遗传算法中交叉率Pc和变异率Pm取值是恒定的，在处理复杂的多变量优化问题时效率不高，并且存在“早熟”的可能性。为此采用自适应遗传算法，自适应PC、Pm能够提供相对某个解的最佳Pc、Pm。该算法在保持群体多样性的同时，可保证遗传算法的收敛能力，有效提高其优化能力。
3．3．1 交叉方式的改进
在交叉方式上，把个体适应度大于群体平均适应度的个体对应于较低的交叉率，使该解得以保护进入下一代：对于低于平均适应度的个体，相对于较高的交叉率，使该解被淘汰。在自适应遗传算法中，交叉率按式(7)进行自适应调整：