基于遗传算法的复杂无源滤波器参数设计
近年来,模拟生物进化过程的遗传算法作为求解优化问题的有效手法而倍受关注。正如ThomasBack等人指出1,同其他手法相比,其优点在于:处理问题的灵活性、适应性、鲁棒性,能取得全局解,对模型要求低,针对不同问题设计的不同遗传算法,不仅能提高现有解的优化品质,还能攻克某些难度大的优化问题。
本文以遗传算法的应用为出发点,提出了一种新的无源滤波器参数设计方法。它能有效克服上述无源滤波器参数设计的困难,十分方便地取得满足性能指标要求的参数设计值。
1 优化模型的建立
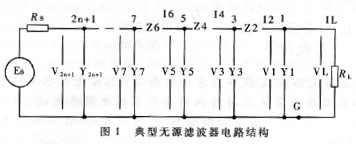
典型的无源滤波器电路组成元件一般按T型结构连接,如图1所示。滤波器的频率特性可以用功率传输函数来定义,即:
其中,X=[X1,X2,...,Xn],为电路的元件参数值矩阵,n为元件总个数,W为频率。若X已知,频率采样点Wi对应的频率特性Li可按下述方法计算:
设 I1=IL=0.1,
V1=ILRL+0=VL
I2=V1Y1+IL
V3=I2Z2+V1
V2n+1=I2nZ2n+V2n-1
I2n+2=V2n+1Y2n+1+I2n
Es=RsI2n+2+V2n+1
用简易的迭代程序求得Es,代入式(1)即可求得Li。
滤波器的结构已知后,先确定结构中的参数取值范围,选择的条件可以比较宽松,然后按预期的性能指标要求,选定适当个频率采样点W1,W2,...,规定其对应功率传输函数幅度界限值,迫使它调整后经过采样点时,满足幅度界限要求(大于、小于或介于)。由此获得的新设计参数X*即是满足预期性能指标的设计值。为求得X*,建立如下优化模型:
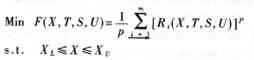
其中,X的定义同前,T=[T1,T2,...]为幅度界限值矩阵,S=[S1,S2,...]为加权系数矩阵,U=[U1,U2,...]为裕度矩阵,XL、XU分别为设计参数的上下界限矩阵。p为偶次方,m为采样点总数,Ri称为余差,具体表达式为:
下界 Ri=Si×Min(+[Li-Ti]-Ui,0)
上界 Ri=Si×Min(-[Li-Ti]-Ui,0)
显然,当存在解X使F函数最小时,Li的值应能控制在Ti的要求范围内,从而使频率特性满足指标要求,因此该解即可视为X*。
2 优化模型的求解
遗传算法是一个强有力的求优算法,它首先随机地产生一组潜在的解X(该解称为"染色体",解的特定集合称为"人口",解中的变量称为"基因"),然后采用生物进化的过程(如染色体交叉变异淘汰等)不断提高解的品质,最后获得最优解。遗传算法有两个重要控制参数--交叉率Pc和变异率Pm对算法的收敛速度有较大影响,文献[3]采用确定不变的Pc和Pm而本文采用随世代数增加而不断自动调整的Pc和Pm。这样做的目的在于:在进化的初期,人口的差异一般较大,交叉率大和变异率小有助于加快收敛,而在进化的后期,交叉率小和变异率大有助防止过早陷入局部最优点。公式如下:
Pc(gen)=Pc(gen-1)-[Pc(0)-0.3]/MAXGEN
Pm(gen)=Pm(gen-1)+[0.3-Pm(0)/MAXGEN
其中,gen表示世代数,MAXGEN表示最大世代数,具体算法如下:
第1步,全局参数设定
给出POP_SIZE(人口数)、Pc(0)、Pm(0)、MAXGEN和设计次数dcnt的大小或范围。
第2步,人口的产生及初使化
设世代数gen=1。以设计参数为变量,组成矩阵X=[X1,X2,...,Xn]。第一代人口由POP_SIZE个染色体构成,每个染色体的基因(即设计参数)在参数各自取值范围内随机产生。
第3步,染色体评价
为了评价代世代中染色体X的优劣,建立染色体适应性评价函数eval(X):
eval(X)={F(X,T,S,U);当X满足约束条件 M,M为一大正数;当X不满足约束条件
对本问题,评价函数越小越好。
第4步,基因操作
通常基因操作有交叉、变异、选择三种(2)。
基因交叉:设交叉计数器ccnt=0,从[0,1]范围内产生随机数rk(k=1,2,...,POP_SIZE),如果rk<Pc(gen),则选择Xk为交叉用;使交叉染色体配对进行如下位交叉操作:
Xj=[X1j,X2j,...,Xpj,...,Xnj] Xj′=[X1j,X2j,...,Xpl,...,Xnl
Xl=[X1l,X2l,...,Xpl,...,Xnl] Xl′=[X1l,X2l,...,Xpj,...,Xnj]
其中Xj、Xl为配对染色体,Xj′、Xl′为交叉后染色体。p为随机选择的交插位
- 基于改进的遗传算法软硬件划分方法研究(07-20)
- 无源三端电路的等效变换(01-26)
- 混合有源电力滤波器的仿真研究(08-03)
- 一种新型无源无损软开关Boost变换器(06-05)
- FL7730应用:TRIAC调光LED驱动器设计指南(独家收录)(07-28)
- 如何设计低成本蜂鸣器?(09-14)
