基于遗传算法的复杂无源滤波器参数设计
其中Xj、Xl为配对染色体,Xj′、Xl′为交叉后染色体。p为随机选择的交插位,接受交叉操作的染色体个数记入ccnt中。
基因变异:设变异计数器mcnt=0,从[0,1]范围内产生随机数rk(k=1,2,...,n×POP_SIZE+n×ccnt),如果rk<Pm(gen),则第k个基因进行变异操作,并使mcnt=mcnt+1。新基因Xk′随机产生于区间[(1-α)Xk,(1+α)Xk];其中1≤i≤POP_SIZE,α为[0,1]范围内选定常数。
染色体选择:计算新生染色体Xn′的评价函数eval(Xn′)(n=1,2,...,ccnt+mcnt 和父代染色体Xn的评价函数evalXn n=12...POP_SIZE ,并按适应性大小排列,选出其中适应性最强的POP_SIZE个染色体构成新一代人口并保留上述过程中最佳染色体V*,这个过程称为"适者生存"选择。
第5步,单次过程结束判断
当F<Er时(Er为一小数量级数值 ,X*=V*,输出X*,转第6步。
当F≤Er且gen≥MAXGEN时,gen=gen+1,返回第3步。
当F≥Er时且gen≥MAXGEN时,返回第2步。
第6步,全过程结束判断
dcnt=dcnt-1;当dcnt>0时,返回第2步;否则,停机。
3 数值实验例
图2为一带通无源滤波器电路结构,通频带要求在950~1050 rad/s之间。为此,每隔5rad/s作一次采样,采样点的幅度大于0.85;设定低频截止频率为800rad/s,幅度小于1e-5;高频截止频率为1300rad/s,幅度小于1e-5。建立如下优化模型:
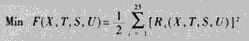
s.t. XL=[0,0,...,0]<X<XU=[18,18,...,18]
其中
X=[X1,X2,...,X19]=[L,C3,C4,L6,L7,C7,L9,L10,C12,L13,C13,L15,L16,C18,L19,C19,L21,L22,C24];
R1=10×Min(+[1.0e-5-L1]-0.0,0),对应W1=800rad/s
Rj=1.0×Min(+[Lj-0.85]-0.05,0);j=2,3,...,22,对应Wj=(5×j+940)rad/s
R23=10×Min(+[1.0e-5-L23]-0.0,0),对应W23=1300rad/s
在NEC4800/210Ⅱ工作站完成上述算法。算法的参数设置为Er=1e-6,α=0.1,Pc=Pc(0)=0.6,Pm(0)=0.1,POP_SIZE=40,MAXGEN=2000,程序语言为UNIX-C。dcnt取10,得到10组设计值,皆能使频率特性满足要求。平均世代数为1508代,平均时间为9.8min。其中一组结果为:
X*=[0.079212.65140.075213.01570.10583.31310.179313.33860.07260.13343.3260.172215.12180.06330.08761.92880.333310.31710.0900]。
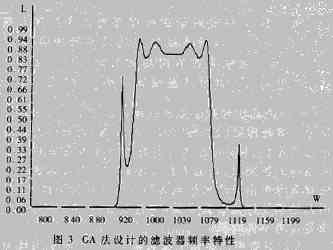
按此参数设计后,滤波器频率特性较好地达到了预期要求,如图3所示。
本文简要分析了无源滤波器参数设计存在困难的主要原因。对无源滤波器的常用电路结构,提出了计算频率特性的简易迭代法,并将求解满足指标要求的参数设计值的问题转化为优化模型的求解过程,使的原来难以描述和解决的设计问题变得明确和简单。
在遗传算法方面,我们并不照搬前人的方法[3],例如,把最小目标函数的求解要求转化为进化的驱动力而不是刻意求得最优解,不仅减少了计算时间,还可提供设计者多种可选择的方案。在遗传算法的变异阶段,采用的是以现有的基因为中心的左右变异方法,有别于常用的在变量范围内变异的方法。因本法中心不断灵活飘移,求解过程出现两个极端,即快速找到合适解或走入死区--永远找不到解。我们通过设定最大世代数消除了后者的可能性,总体上提高了效率。
本法有效地克服了无源滤波器参数设计的困难,具有普遍性的价值和意义。其基本思想及原理亦可在电气、电子、自动化等较复杂系统的参数设计领域得到广泛的应用。
- 基于改进的遗传算法软硬件划分方法研究(07-20)
- 无源三端电路的等效变换(01-26)
- 混合有源电力滤波器的仿真研究(08-03)
- 一种新型无源无损软开关Boost变换器(06-05)
- FL7730应用:TRIAC调光LED驱动器设计指南(独家收录)(07-28)
- 如何设计低成本蜂鸣器?(09-14)
