最坏情况电路设计对元件容差的考虑

28kΩ;

5、选择RP=500Ω。

最终得到的阻值为：R=820Ω，RP=500Ω。有些工程师认为，最坏情况的设计程序太严格，而且要使用的电位器阻值较大，分辨率较低，电位器漂移误差较大。有可能解决这一问题的一种方法是冒险降低电位器阻值，不过更好的解决方法是使用精度更高的部件。非比例电路必须考虑最大容差的偏移，因此，一个5%的购买容差会导致20% (±10%)的总容差。

比例计量电路

图2和公式1中的分压器是典型的比例计量电路。参照容差公式，你可以看到容差的某些部分在公式中相消。

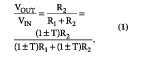
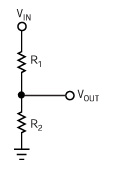
图2，比例电路可消去电阻器阻值的某些容差。

为了得到最大增益值，你要把R2的容差设定得大，而把R1的容差设定得小。由于R2的容差大，它就以(1+T)R2的形式出现在公式的各部分中。表2以四种电阻器比例列出了理想增益、最大增益和百分比误差。要注意的是，当R1=R2时出现最小增益误差，而且该增益误差等于容差。该非比例电路必须取两倍容差，即2T，而比例电路只取容差T。

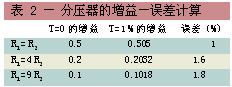
当分压器中两只电阻器的容差同时很大或很小时，两种容差就会相消。如果电阻器制造商保证在环境温度变化时所有电阻器以相同方向按比例漂移，则温度 容差也会相消。

差分放大器：自行其是

许多参考文献说，你不可能用分立元件制作一个CMR(共模抑制)良好的精密差分放大器。差分放大器的容差分析说明了为什么这种说法是正确的。考虑图3和公式2(参考文献1)中的差分放大器电路，假设该放大器是理想的。

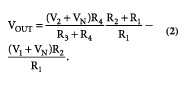
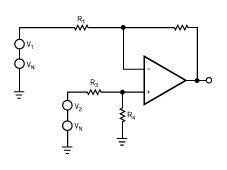
图3，差分放大器利用比例电阻器来得到很高的CMR。

该电路的CMR是在无信号时测量的，所以V1=V2=0.0，公式2变成公式3：

当R1=R3和R2=R4时，增益为零，CMR为无穷大。实际上，电阻器容差和运算放大器误差总是将CMR限制在大约100 dB以下。将公式3改写为公式4，就使你的注意力集中到差分增益和电阻器容差上。公式4包含4个电阻器容差，因此有16个可能的误差因子。如果你研究所有的可能性，就会看到误差范围从所有电阻器容差向同一方向变化时的零一直到2T/(1-T)。

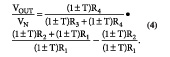
当总容差为1%(对0.5%电阻器来说，为P+D)时，电阻器容差可以导致CMR的范围从高达运算放大器极限值到低至-34.89dB。考虑到1%电阻器的购买容差和漂移容差，总的CMR可能低至-24.17 dB。你可以将这一误差作为CMR误差来计算，不过，在没有共模电压而有差分输入信号的情况下，这一误差就变成增益误差。

采用分立元件的差分放大器是难以制作和微调的，所以大多数设计师都使用具有内置微调电阻器的IC差分放大器。廉价的IC差分放大器具有高达-86dB 的CMR。

你在分析电路以确保长期性能和可制造性时，要切记无源元件具有购买容差和漂移容差，而且漂移容差可能大于购买容差。你可以在制造过程结束时微调购买容差，但是，你或你的系统只能在进行测量之前调节漂移容差。非比例电路要取两倍的电阻器容差，而比例电路可以将误差降低到容差值。精确的差分放大器难以用分立器件制造，但是具有电阻器微调和匹配功能的IC通常可以得到-90 dB的CMR。