利用基于FPGA 的模糊控制器控制蔗糖提取

采用赛灵思 Virtex-6 FPGA 实现的三输入模糊控制器可在甘蔗制糖过程中保持甘蔗水平高度。

食糖是日常生活中广泛使用的重要食品配料成分。全球一半以上的原糖都从甘蔗中榨取获得。印度是仅次于巴西的世界第二大食糖生产国，从事甘蔗种植的农民及其家属数量有 6000 万，产值达 120 亿美元。

由于甘蔗汁的提取是非线性过程，因此我们的团队将模糊逻辑作为改善流量的方法。Mody 科技大学 (MITS) 研究人员的分析表明，利用赛灵思 FPGA 设计和实现的模糊控制器的性能优于传统控制器。如果每天压榨 2,500 吨甘蔗，就需要 26.6 kg/s 的流速。

在具体研究如何实现三输入模糊控制器之前，我们有必要了解食糖制造的基本知识。

如何提取甘蔗

图 1 给出了甘蔗汁提取流程图。甘蔗坯料是指制糖厂把从甘蔗种植者手中收购来的甘蔗进行称重，并卸在院子内。利用起重机将甘蔗放在传送带上。甘蔗传送带不断移动，负责将甘蔗送到食糖生产厂房内。

甘蔗首先通过两组旋转切刀。切刀将甘蔗切成小段，然后撕蔗机将小段甘蔗切成小块纤维。倾斜传送带将这些大约 1-2cm 的甘蔗块送入 Donnelly 榨糖机。压榨机的两三个压辊对甘蔗块进行压榨以提取甘蔗汁。该过程在五六套压榨机中重复进行。剩余的残留物称为甘蔗渣,被送到锅炉中作为燃料使用；提取的甘蔗汁需要送去净化，然后送到蒸发器中做成蔗糖。

待加工的甘蔗非常不均匀，在提取汁液过程中会对压榨机效率产生不利影响，可导致压榨机故障、停机和设备堵塞。为了获得最佳的甘蔗汁提取效果，有必要使 Donnelly 榨糖机中的甘蔗水平面保持所需的高度。

我们希望模糊逻辑比传统控制器更好地改变倾斜传送带的速度，以消除甘蔗供给不均的问题并保持所需的甘蔗水平高度。这就是为什么我们尝试将模糊逻辑概念引入制糖领域。

2014 年，我们所做的第一步是设计一款双输入模糊控制器[1]，用来精确监测两个参数的变化：倾斜传送带上的甘蔗重量以及 Donnelly 榨糖机中的甘蔗高度。该控制器的作用是保持榨糖机中的恒定高度，以维持所需的26.6kg/s 的流速。当我们将检测结果与传统控制器的结果进行对比时，可清楚看到双输入模糊控制器的效果要好得多。由于甘蔗在辊子间被压碎，因此我们决定在相同算法中导入第三个参数——辊速——作为实验参数。在加入第三个参数辊速后表明，该变量与其他两个变量同样重要。
因此，2014 年我们将辊速作为第三个参数[2]。我们利用这个附加参数重新设计了算法，并使用 MATLAB® 实现。当新型三输入控制器软件实现方案完成后[3]，下一步是实现算法和使用赛灵思 FPGA 开发整个模糊系统。FPGA 这种可重编程芯片能够对电子电路进行实时的硬件实现。这种芯片非常可靠，性价比高，而且可在制造之前检查电路性能。因此，赛灵思 Virtex®-6 FPGA 成为了完美的硬件实现解决方案。

硬件设计

图 2 给出了三输入模糊控制器的算法。三输入模糊控制器的控制原理与双输入版本相同，只是根据三个输入进行修改，并在 MATLAB 上实现。控制原理为：控制器控制重量、高度和辊速的三个速度等级，即低辊速(RL：12cm/s)，中辊速(RM：14.3cm/s)和高辊速(RR：16.6cm/s)。

在 MATLAB 上设计控制器后，下一步是设计用于测量输入参数所需的硬件。称重传感器用于测量倾斜传送带上的甘蔗量。为了测量榨糖机中的甘蔗水平高度，我们在设计中添加了高度传感器。测速发电机用于测量辊子的旋转速度。

称重传感器、高度传感器和测速发电机的输出仅为微伏。为了能在接下来的步骤中使用这些指标，我们必须将输出电压值放大成可测量的电平，也就是从微伏变为毫伏。我们使用 PSpice 上的信号调节系统来进行放大。接下来，我们利用与调节系统串联的模数转换器 (ADC) 将结果转为数字值。这样，放大后的输入就被送到控制器中。

五步过程

使用赛灵思硬件的模糊控制器的 VHDL 实现过程分为五个步骤：输入模糊化、规则评估、逻辑蕴涵、聚合和去模糊化。
设计模糊逻辑控制器有两种方法，即 Mamdani 和 Sugeno。Mamdani 法难度大而且非常复杂。根据研究显示，Mamdani 方法需要通过对不断变化的函数进行积分来得到二维形状的几何中心。因此，这种方法在计算上不够高效。另一方面，而 Sugeno 设计方法则简单得多。因此，我们采用了 Sugeno 实现方法。

第一步是模糊化，包括将明确值转换为模糊值，然后由隶属函数代表。明确值为特定集；模糊值属于特定范围但不限于特定集内。

三个输入变量分别是重量、高度和辊速。使用三角隶属函数来代表这些输入变量。输入参数“重量”的论域为 500kg-1,000kg，它被模糊化为 11 个三角语言变量 (LV)。输入参数“高度”的论域为 0-180cm，它被模糊化为 7 个三角语言变量(LV)。输入参数“辊速”的论域为 12cm/s-16.6cm/s，它被模糊化为 3 个三角语言变量(LV)。

VHDL 代码方面的模糊化如下所示。我们用三个点和两个斜率定义每个隶属函数，如图 3 所示。使用下列等式计算上斜率（斜率 1）和下斜率（斜率 2）：

S1= (y2-y1/Point2-x1) S2= (y2-y1/x2- Point 2)

隶属度 (DOM) 函数 (μ) 是模糊化的下一步。我们的算法将隶属函数分成四个部分，即 Segment-1(μ=0),Segment-2{(Input - point 1)* slope 1},Segment-3{(Input-point 2)* slope 2} 以及 Segment-4 (μ=0)。DOM 值计算如下：

•        如果输入值 < Point 1 (Segment 1)，那么 DOM =0。
•        如果输入值 ≤ Point 2，且 ≥ Point 1 (Segment 2)，那么 DOM = (Input-Point 1) * Slope 1。
•        如果输入值 ≤ Point 3，且 ≥ Point 1 (Segment 3)，那么 DOM = FF- (Input–Point 2) * Slope 2。
•        如果输入值 ≥ Point 3 (Segment 4)，那么 DOM = 0。


用于锅炉的甘蔗渣


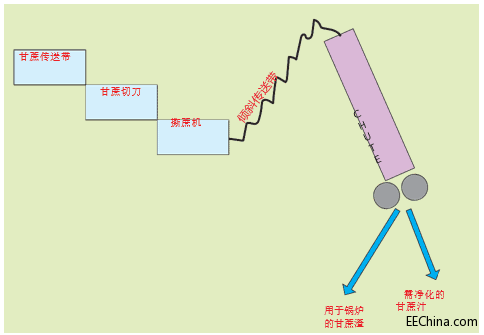
图 1–甘蔗汁提取流程图


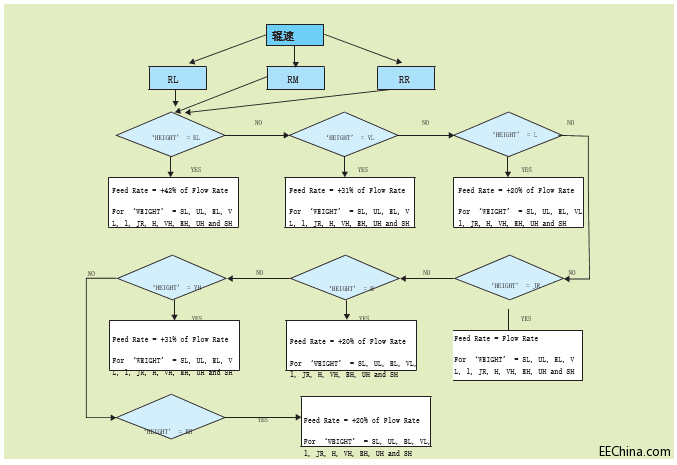
图 2：三输入模糊控制器算法开发


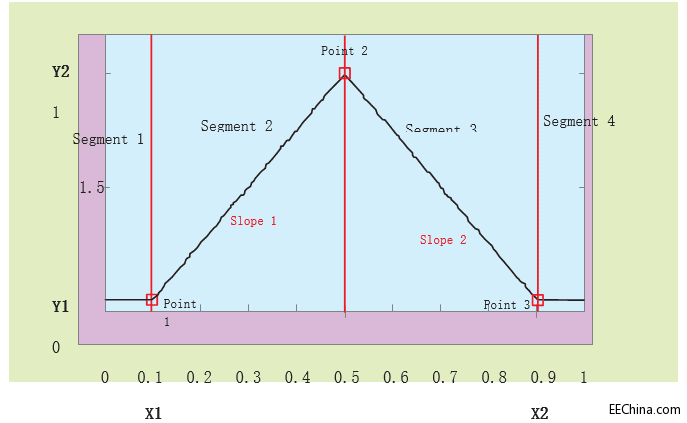
图 3：由三个点和两个斜率定义的隶属函数

不同的隶属度

下一步是规则设计，以确定为响应不同隶属度函数所采取的行动。使用简单的 If-Then 条件构成模糊规则，其中每个先行词 (antecedent) 都有结果。MATLAB 中的“Fuzzy Logic Toolbox”提供用以组合多个先行词的不同运算符。我们选择 AND 运算符将三个先行词进行组合，因为它的多个先行词运算最少。对于三输入控制器而言，总共生成 231 条规则。我们为这些规则设计了一个规格表。最小值函数可以找到三个值中的最小值，即计算出三个输入变量中的最小 DOM 值。

我们还发现很多规则的结果是相同的。收集所有具有相同结果的规则，并使用最大值函数计算这些值中的最大数。下一步，我们收集所有具有相同结果的规则。编写不同的最大值函数用以评估整个语言变量(LV)的最大值。

在识别每个规则的输出之后，最后一步是将所有输出整合成单个值，换句话说，就是将这些值转换为确定值。这可通过去模糊化来完成。

去模糊化是模糊系统设计中的最后一步也是重要的一步。去模糊化的值可用来生成一个确定值，它就是倾斜电机的速度。我们所用的 Sugeno 去模糊法属于加权平均法。在该方法中，我们将从聚合中获得的模糊输出与相应的单个值相乘，然后用这些值的总和除以从规则评估中获得的所有模糊输出（也就是聚合后获得的值）的总和。

VIRTEX-6 实现

在实现以上步骤后，我们成功使用三角从属函数和中心去模糊法设计出一种三输入模糊控制器。程序代码已经由作者提供。我们使用 MATLAB 7.11.0.584 版本 (R2020b) 的 Fuzzy Toolbox 仿真三输入模糊控制器，并利用赛灵思的 ISE® Design Suite


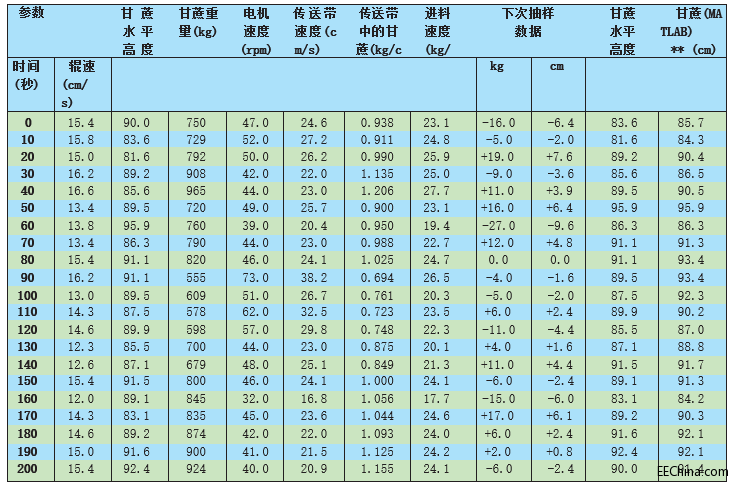
* FPGA 实现的系统每次抽样后的甘蔗高度   ** MATLAB 实现的系统每次抽样后的甘蔗高度

表 1–甘蔗高度在 90cm 时，每次抽样辊速都不同。

14.5 并使用 VHDL 在赛灵思 Virtex-6 FPGA上 将其实现。采样周期为10 秒，仿真总时长为 200 秒。

我们调差了六个不同情况下总共 756 种不同的输入参数条件，但我们重点研究的是仿真最初阶段传送带上甘蔗高度和甘蔗重量分别为 90cm 和 750kg 的这种情况。辊速在每次抽样时均有所变化。表 1 给出了仿真结果。

硬件实现步骤包括在我们 MITS 校园实验室中进行的 VHDL 建模、仿真、综合和 FPGA 实现。我们使用混合型建模方法来设计三输入模糊控制器的 VHDL 模型，其中包括行为建模和结构建模。该设计在赛灵思的 ISim 仿真器上进行仿真。ISim 生成的波形用来验证控制器的功能。图 4 给出了倾斜传送带中甘蔗重量为 750kg，Donnelly 榨糖机中甘蔗高度为 90cm，辊速为 16.6cm/s 时的仿真波形。在这些条件下，期望的倾斜电机速度为 54.2rpm (MATLAB)。去模糊化仿真结果为 36H 或 54 rpm,与 MATLAB 结果匹配,并验证了设计。


图 4：当重量为 750kg，高度为 90cm，辊速为 16.6 cm/s 时的仿真波形

仿真之后，我们对设计进行综合，以生成技术原理图和粗略的器件利用报告。我们发现我们的设计使用了 78% 以上的 Virtex-6 Slice 查找表 (LUT)，93% 的已占用 Slice，1% 的 Slice 寄存器，以及 1% 的 LUT 触发器。


表 2–结果对比

然后，我们将 VHDL 结果与传统控制器结果进行对比（见表 2）。对比结果表明模糊逻辑系统比传统控制器效率更高。
位于 MITS 的实验室提供一块用于研究的 Spartan®-6 FPGA。然而，我们发现所需的 LUT 模块数量超出了目标器件的容量。这就是为什么我们转而在 Virtex-6 上实现设计。但是，由于缺少资源，我们无法在实验室中进行实时实现。下一步中，我们希望与印度国家制糖学会管理部门联合开发整个系统，并在真实环境中验证结果。我们已经向印度国家制糖学会交付方案演示，并收到了正面回应。我们坚信模糊逻辑概念很有可能改变制糖工业的未来。

参考资料
1.        Y. Misra 与 H.R.Kamath 共同编撰的“为保持制糖过程中甘蔗的水平高度专门设计一种传统模糊控制器算法”，摘自《智能系统与应用国际期刊》，期刊编号：2074-9058，第 7 卷第 1 章，2014 年 12 月

2.        Y. Misra 与 H.R.Kamath 共同编撰的“《在使用 VHDL 的 FPGA 中对三输入传统控制器进行实现方案与性能分析，以确保甘蔗压榨过程中甘蔗水平高度”， 摘自《工程研究与技术国际期刊》(IJERT)，期刊编号：2278-0181，第 3 卷第 9 期，2014 年 9 月

3.        Y. Misra 与 H.R.Kamath 共同编撰的“对用于保持制糖过程中甘蔗高度的三输入模糊系统进行分析和设计”， 摘自《自动化控制杂志》（已接受），期刊编号：2372-3041