利用Xilinx FPGA实现高效并行实时上采样
时间:01-12
来源:互联网
点击:
本文介绍一种使用Virtex-6器件和免费WebPACK工具实现实时四倍上采样的方法。
作者:William D. Richard
圣路易斯华盛顿大学副教授
wdr@wustl.edu
许多信号处理应用都需要进行上采样。从概念上讲,对数据向量进行M倍上采样的最简单方法是用实际频率分量数的(M-1)倍个零填充数据向量的离散傅里叶变换(DFT)[1],然后将零填充向量转换回时域[1,2]。但这种方法计算量很大,因此不能在FPGA内部高效实现。在本文介绍的高效并行实时上采样电路中,每个ADC时钟可产生M个上采样值,其中M是所需的上采样倍数。在我们赛灵思的Virtex®-6 XC6VLX75T FPGA实现方案中,上采样倍数M为4,可以作为较普遍方法的一个实例。
我们并行上采样方法的总体概念源于某些作者所称的“窗口SINC插值”,这种方法在文献资料[3,4]中有一些非常精彩的专文介绍。
为了更好的说明,现以图1中所示的16MHz模拟信号为例。该信号的表达式为:
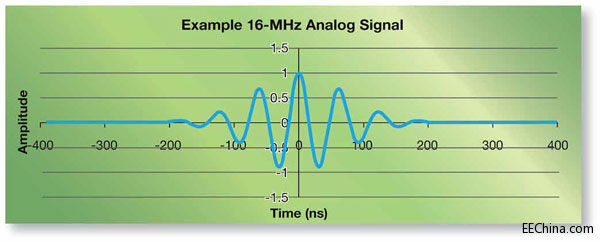
图1 - 展示上采样过程的16MHz信号实例
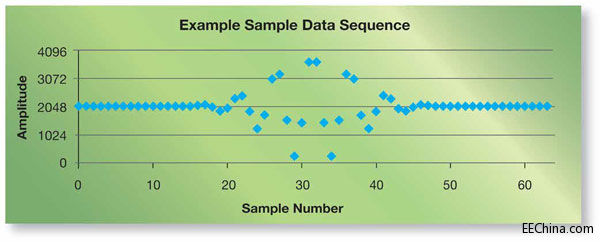
图2 - 本图是12位ADC,输入范围为ADC完整输入范围的97.7%,用80MHz或每周期五次频率对图1的模拟信号采样得到
的样本数据序列实例。
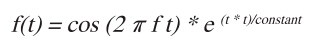
等式 1
如果用12位ADC以80MHz的频率对图1所示的信号进行采样或量化,输入范围为ADC完整输入范围的97.7%,则每个信号周期只能采样五次,产生的样本数据序列如图2所示。如果对该示例数据序列进行四倍上采样,则有效采样率为320MHz,每个信号周期能够提供20个样本。虽然您可以使用本文介绍的方法进行更高倍数的上采样,但为了说明起见我们还是使用M=4的上采样。
当然,还可以通过直接在ADC生成的数据序列的每个实际样本值之间插入(M-1)个零来获得上采样数据向量及所需的样本数(公认效果较差)。该“零插入步骤”对应于复制频域中的原始信号频谱。通过对得到的“零填充”时域信号进行低通滤波,就能去除频域中所需频谱的“复本”,从而获得上采样数据向量。
FIR滤波器设计
频域中的理想(砖墙式)低通滤波器相当于在时域中用无限域Sinc函数作卷积。因此为近似化所需的卷积运算,可让前述的零填充时域信号通过速率为ADC时钟频率M倍的对称低通FIR滤波器,该滤波器拓扑结构与图3所示的示例31抽头FIR滤波器相同。用这种方法,我们可以实时生成上采样数据向量。图3中的R1、R2、...、R31代表速率为ADC时钟频率M倍的寄存器,C0、C1、…、C15代表FIR滤波器的系数。
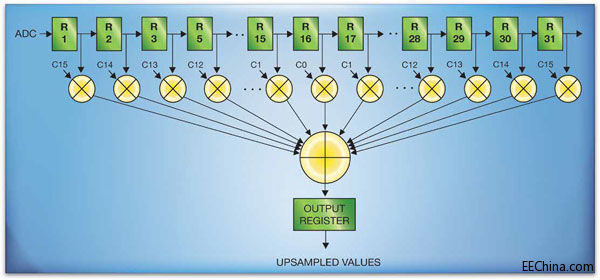
图3 - 当滤波器工作在基本ADC时钟频率的M倍频率时,零插入步骤中使用31抽头FIR滤波器每时钟周期可生成一
个上采样数据值
需要说明的是,图3所示的FIR滤波器中的大部分寄存器在任何特定时钟间隔内都会包含0,而非实际的样本数据。以M=4为例,当R1包含实际样本数据时,R2、R3和R4将包含0。当R1包含实际样本数据时,R5、R9、R13、R17、R21、R25和R29也将包含实际样本数据,其余的寄存器将包含0。在下一时钟间隔中,R2、R6、R10、R14、R18、R22、R26和R30将包含实际样本数据。
如图3所示,由于在通过FIR滤波器的每M个样本中有M-1个样本为0,就M=4、使用31抽头FIR滤波器的情况而言(如图4所示),您可以将滤波器分解开,并行产生M个输出。采用这种实现方案,并行FIR滤波器的工作频率为ADC的基本时钟频率,而非ADC时钟频率的M倍。
如图4所示,您可以设定窗口SINC函数的系数Cw(n)来最大限度地减少实现该FIR滤波器所需的乘法器数量。对于T个抽头的低通FIR滤波器而言,可通过下式得出最佳系数:
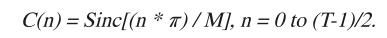
等式2
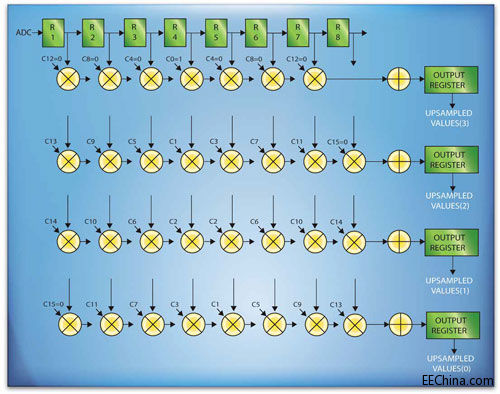
图4 - 通过在任何给定时钟周期内对图3中每四个寄存器中唯一一个包含非零数据的寄存器进行观察,可以拆解该滤波器,再让滤波器在以基础ADC时钟频率运行的情况下并行
这里的汉宁窗系数的计算方法为:
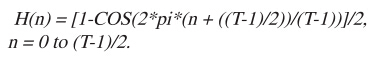
等式3
窗口SINC函数系数Cw(n)随即通过对应的C(n)和H(n)值相乘即可得到,如:
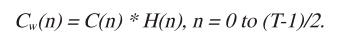
等式 4
在M=4时,如果按上面介绍的方法计算31抽头FIR滤波器的系数,令C0=1.0,C4=C8=C12=C15=0,则无需使用与图4中这些系数有关的9个乘法器。此外,由于生成UPSAMPLED VALUE(1)每个系数会使用两次,用户可以“折叠”该实现方案,比如在相乘之前让R1和R8相加,这样就可以去掉四个乘法器。最后得到的设计仅使用18个乘法器每时钟周期就可产生四个上采样值。需要注意的是按上文介绍的设计方法,每个原始样本值会原样从并联滤波器输出。
我们使用图5所示的可综合VHDL[5]模型评估图4所示电路的性能。该VHDL实现方案假定样本数据为12位,即可能来自美国模拟器件公司的AD9670八通道超声前端集成电路[6]的数据。滤波器系数表达为25位定点常数,以与集成到FPGA芯片上的乘法器输入位数相匹配。来自ADC的输入样本先馈入与输入引脚相连的寄存器(图4中的R1),上采样输出值则使用与输出引脚相连的寄存器。寄存器R2到R8属芯片内部寄存器。寄存器R1到R8故意设定为15位宽度,以便为综合后逻辑提供执行计算所需的动态余量。该设计能检查溢出或下溢,还能将结果钳制在有效范围以内。
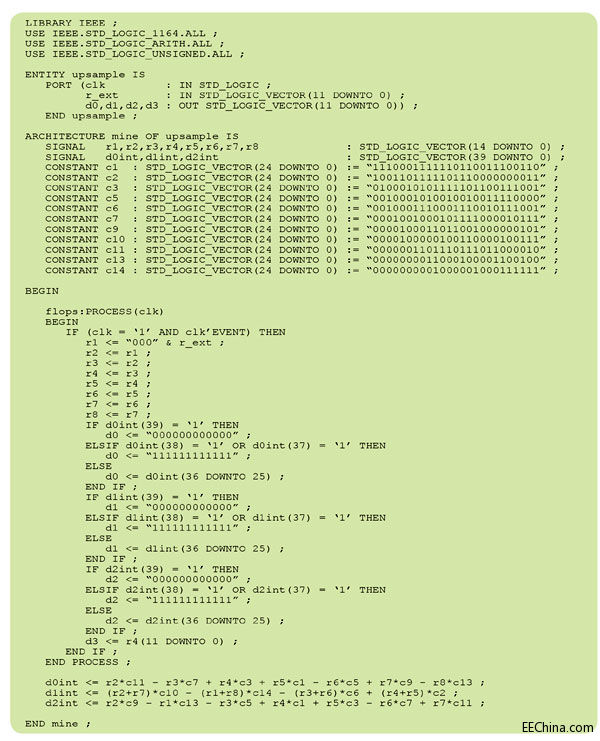
图5 - 该VHDL源代码使用单进程和25位定点系数实现图4的滤波器拓扑结构。
作者:William D. Richard
圣路易斯华盛顿大学副教授
wdr@wustl.edu
许多信号处理应用都需要进行上采样。从概念上讲,对数据向量进行M倍上采样的最简单方法是用实际频率分量数的(M-1)倍个零填充数据向量的离散傅里叶变换(DFT)[1],然后将零填充向量转换回时域[1,2]。但这种方法计算量很大,因此不能在FPGA内部高效实现。在本文介绍的高效并行实时上采样电路中,每个ADC时钟可产生M个上采样值,其中M是所需的上采样倍数。在我们赛灵思的Virtex®-6 XC6VLX75T FPGA实现方案中,上采样倍数M为4,可以作为较普遍方法的一个实例。
我们并行上采样方法的总体概念源于某些作者所称的“窗口SINC插值”,这种方法在文献资料[3,4]中有一些非常精彩的专文介绍。
为了更好的说明,现以图1中所示的16MHz模拟信号为例。该信号的表达式为:

图1 - 展示上采样过程的16MHz信号实例

图2 - 本图是12位ADC,输入范围为ADC完整输入范围的97.7%,用80MHz或每周期五次频率对图1的模拟信号采样得到
的样本数据序列实例。
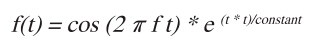
等式 1
如果用12位ADC以80MHz的频率对图1所示的信号进行采样或量化,输入范围为ADC完整输入范围的97.7%,则每个信号周期只能采样五次,产生的样本数据序列如图2所示。如果对该示例数据序列进行四倍上采样,则有效采样率为320MHz,每个信号周期能够提供20个样本。虽然您可以使用本文介绍的方法进行更高倍数的上采样,但为了说明起见我们还是使用M=4的上采样。
当然,还可以通过直接在ADC生成的数据序列的每个实际样本值之间插入(M-1)个零来获得上采样数据向量及所需的样本数(公认效果较差)。该“零插入步骤”对应于复制频域中的原始信号频谱。通过对得到的“零填充”时域信号进行低通滤波,就能去除频域中所需频谱的“复本”,从而获得上采样数据向量。
FIR滤波器设计
频域中的理想(砖墙式)低通滤波器相当于在时域中用无限域Sinc函数作卷积。因此为近似化所需的卷积运算,可让前述的零填充时域信号通过速率为ADC时钟频率M倍的对称低通FIR滤波器,该滤波器拓扑结构与图3所示的示例31抽头FIR滤波器相同。用这种方法,我们可以实时生成上采样数据向量。图3中的R1、R2、...、R31代表速率为ADC时钟频率M倍的寄存器,C0、C1、…、C15代表FIR滤波器的系数。

图3 - 当滤波器工作在基本ADC时钟频率的M倍频率时,零插入步骤中使用31抽头FIR滤波器每时钟周期可生成一
个上采样数据值
需要说明的是,图3所示的FIR滤波器中的大部分寄存器在任何特定时钟间隔内都会包含0,而非实际的样本数据。以M=4为例,当R1包含实际样本数据时,R2、R3和R4将包含0。当R1包含实际样本数据时,R5、R9、R13、R17、R21、R25和R29也将包含实际样本数据,其余的寄存器将包含0。在下一时钟间隔中,R2、R6、R10、R14、R18、R22、R26和R30将包含实际样本数据。
如图3所示,由于在通过FIR滤波器的每M个样本中有M-1个样本为0,就M=4、使用31抽头FIR滤波器的情况而言(如图4所示),您可以将滤波器分解开,并行产生M个输出。采用这种实现方案,并行FIR滤波器的工作频率为ADC的基本时钟频率,而非ADC时钟频率的M倍。
如图4所示,您可以设定窗口SINC函数的系数Cw(n)来最大限度地减少实现该FIR滤波器所需的乘法器数量。对于T个抽头的低通FIR滤波器而言,可通过下式得出最佳系数:
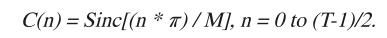
等式2

图4 - 通过在任何给定时钟周期内对图3中每四个寄存器中唯一一个包含非零数据的寄存器进行观察,可以拆解该滤波器,再让滤波器在以基础ADC时钟频率运行的情况下并行
这里的汉宁窗系数的计算方法为:
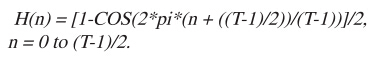
等式3
窗口SINC函数系数Cw(n)随即通过对应的C(n)和H(n)值相乘即可得到,如:
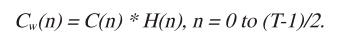
等式 4
在M=4时,如果按上面介绍的方法计算31抽头FIR滤波器的系数,令C0=1.0,C4=C8=C12=C15=0,则无需使用与图4中这些系数有关的9个乘法器。此外,由于生成UPSAMPLED VALUE(1)每个系数会使用两次,用户可以“折叠”该实现方案,比如在相乘之前让R1和R8相加,这样就可以去掉四个乘法器。最后得到的设计仅使用18个乘法器每时钟周期就可产生四个上采样值。需要注意的是按上文介绍的设计方法,每个原始样本值会原样从并联滤波器输出。
我们使用图5所示的可综合VHDL[5]模型评估图4所示电路的性能。该VHDL实现方案假定样本数据为12位,即可能来自美国模拟器件公司的AD9670八通道超声前端集成电路[6]的数据。滤波器系数表达为25位定点常数,以与集成到FPGA芯片上的乘法器输入位数相匹配。来自ADC的输入样本先馈入与输入引脚相连的寄存器(图4中的R1),上采样输出值则使用与输出引脚相连的寄存器。寄存器R2到R8属芯片内部寄存器。寄存器R1到R8故意设定为15位宽度,以便为综合后逻辑提供执行计算所需的动态余量。该设计能检查溢出或下溢,还能将结果钳制在有效范围以内。

图5 - 该VHDL源代码使用单进程和25位定点系数实现图4的滤波器拓扑结构。
FPGA 电路 ADC 赛灵思 滤波器 低通滤波器 LED VHDL 集成电路 仿真 DSP 相关文章:
- 基于FPGA的片上系统的无线保密通信终端(02-16)
- 基于Virtex-5 FPGA设计Gbps无线通信基站(05-12)
- 基于FPGA的DVI/HDMI接口实现(05-13)
- 基于ARM的嵌入式系统中从串配置FPGA的实现(06-09)
- 采用EEPROM对大容量FPGA芯片数据实现串行加载(03-18)
- 赛灵思:可编程逻辑不仅已是大势所趋,而且势不可挡(07-24)
