Simulink软件平台仿真LUTs技术实现NCOs
时间:11-09
来源:互联网
点击:
数控振荡器(Numerically Controlled Oscillators,NCOs)是软件无线电的重要组成部分和研究内容,它广泛应用于DSP中,如通信领域的信号调制解调,蜂窝电话、基站、雷达系统、数字电视、GPS和无线LAN等。
NCOs可以通过各种方式实现:无限冲击响应滤波器(IIR filters),坐标旋转(CORDIC rotations),查找表技术(Lookup Tables,LUTs)。本文在Simulink软件平台仿真LUTs技术实现NCOs时,累加器步长、累加器控制字等参数对NCOs性能的影响。重点讨论NCOs的频谱纯度问题,即如何抑制杂波分量,影响频谱纯度的因素以及如何提高无杂散动态范围(SpuriousFree Dynamic Range,SFDR)。
1 NCOs的工作原理
NCOs主要包括一个正弦波样点查找表(LUTs)和一个产生地址的累加器,如图1所示。
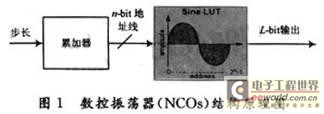
图1中n为累加器产生的地址位数,则LUTs有N=2n个输入。LUTs的输出分辨率/精度为L位(该参数与n有关),其工作原理见图2。
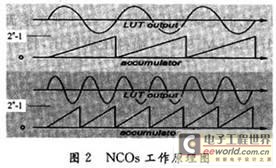
由图2可以看出,累加器产生地址码,循环从LUTs地址中取数正弦波的样点数据,其取数的速率越快,即步长μ越大,则产生的正弦波频率越高。
设步长参数μ由式(1)决定:

式中:N为LUTs的样点数据总量;fs为系统采样频率;fd为期望的正弦波的频率。
例如,累加器地址数据线宽度为8 b,则对应的LUTs的数据样点数为N=2n=256。如果采样频率为10 MHz,期望频率为2.5 MHz,则步长为:
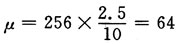
2 提高NCOs的无杂散动态范围
SFDR是无线系统设计中需要考虑的重要参数。如果振荡器产生的信号包含过多的杂波(Spurs)频率,这些干扰成分会使信号混频的质量变差,特别是当杂波频率接近中心频率时,在后续的电路中很难去除。
2.1 相位截断对频谱纯度的影响
当LUT输出正弦波样点数据时,只有整数部分可以用于输出,而小数部分则被忽略,这导致输出相位部分有截断。相位截断(Phase Truncation)的情况决定了产生的正弦波的纯度。如:当采样频率为100 kHz时,NCOs输出的期望频率为24.3 kHz,其NCOs设置参数见表1。从表1中可以看出,LUTs的分辨率为32 b,则可以忽略幅度值量化的影响,而杂波主要是由相位截断产生的。
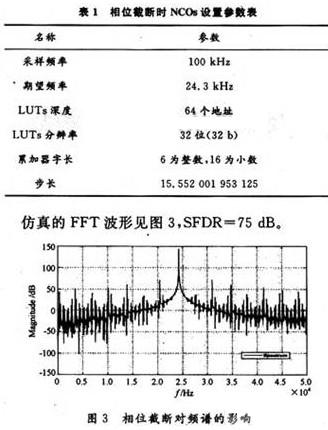
2.2 幅度值量化对频谱纯度的影响
将LUT的深度增大为12 b(4 096),则可以忽略相位舍去对频谱纯度的影响,而杂波主要由幅度值的量化(Amplitude Quantization)产生。同样,当采样频率为100 kHz时,NCOs输出的期望频率24.3 kHz,NCOs设置参数见表2。
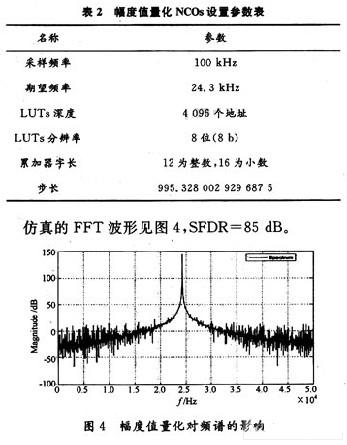
由图3,图4可以看出,相位截断产生的杂波远大于幅度值量化产生的杂波,是杂波的主要来源。
由以上的仿真波形可以看出,提高整数位的位数,虽然可以使相位截断小,频率杂波少,但要使用较大的LUTs容量。如整数位增加一位,即由n位增加n+1位,则LUTs的数据量会增加一倍。
提高小数位的位数可以有较高的步长精度和频率分辨率,但需要更加多的累加器。如小数部分由b位增加到b+1位,虽然对LUTs无影响,但将累加器的加法器和延迟器分别增加1位,从而影响NCOs的输出频率。
提高LUTs输出分辨率对正弦波样点的幅度值量化影响小,但需要更多的LUTs存储器。如LUTs输出分辨率增加1位,由L位增加L+1 位,LUTs所需的存储容量扩大2n。
可见,采用传统的设计方法要达到无相位截断,则需要LUT的字长非常长,占用资源非常大,导致NCOs的成本很高,而这在实际实现过程中是不可行的。
2.3 相位加抖提高SFDR
通过以上的仿真研究可看出,虽然可以通过增加整数位和提高LUTs输出分辨率的方法来提高SFDR,但因它们要占用大量的资源,因而不是经济有效的方法。为有效解决杂波问题,必须考虑其他有效的方法。目前的主要技术手段有:
幅度加抖(Amplitude Dithering):在LUT的输出中加入低水平的噪声,以打散原有幅度值量化的噪声结构。
相位加抖(Phase Dithering):在累加器的输出中加入低水平的噪声,以打散原有相位截断的噪声结构。
带通滤波(Bandpass Filtering):在振荡器输出端加滤波器滤出毛刺频率。但该方法很难滤出靠近中心频率的杂波。
以上的仿真已经证明,相位截断对SFDR的影响量是最大的,是提高SFDR的首选方法。
相位加抖的数学模型如图5所示。在LUTs地址字截断之前,在累加器的输出中加入低水平的伪随机噪声(A Low-level of Pseudo Random Noise),其中抖动的位数d是可变的。
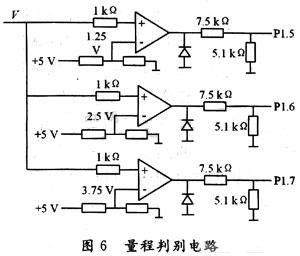
抖动(Dither)可以通过线性反馈移位寄存器(Linear Feedback Shift Register,LFSR)来实现,见图6。LFSR有带M个抽头的移位寄存器,抽头反馈通常由或门构成,以产生一个周期为2M-1的序列。因此,长伪随机噪声序列(Long Pseudo Random Noise Sequences)可以用很少的硬件资源实现。例如,一个由12个元件构成的LFSR能够生成周期为4 095的PN序列。LFSR可以由M个D触发器和很少的组合器件构成。
来自某位的抽头,可以组合为一个矢量生成该位的抖动。实际实现时,可以采用较长的移位寄存器。移位寄存器越长,则输出的抖动越接近随机的性质。
下面分析相位加抖数据位数d对SFDR的影响。图7~图9分别为d=b-3,b+3,b三种情况的仿真波形,其中b为累加器控制字小数部分的位数。
加抖位数d=6-3时,仅对整数位产生0~1/8的影响。此时将SFDR提高了1 dB。可见,增加过少位数的抖动,仅对相位的截断有很小的影响,对改变杂波极为有限。
加抖位数d=b+3时,可以对整数位产生0~8的影响。此时将SFDR提高了9 dB。但同时可以看到,由于增加抖动的位数过多,虽然消除了杂波,但同时也提高了整个频谱的噪声电平。
加抖位数d=b时,可以对整个整数位产生0~1影响。此时将SFDR提高到106 dB。同时可以看到,由于增加抖动的位数恰当,既消除了杂波,又提高了整个频谱的噪声电平。
在用FPGA实现NCOs时,通过相位加噪可以提高整个输出频率的SFDR性能。但从图3,图6比较可以看出,在整个电路中串入了加法器,且关键路径包含了两个部分Dithering和NCOs的加法器,因而限制了整个设计的最大时钟频率。
NCOs可以通过各种方式实现:无限冲击响应滤波器(IIR filters),坐标旋转(CORDIC rotations),查找表技术(Lookup Tables,LUTs)。本文在Simulink软件平台仿真LUTs技术实现NCOs时,累加器步长、累加器控制字等参数对NCOs性能的影响。重点讨论NCOs的频谱纯度问题,即如何抑制杂波分量,影响频谱纯度的因素以及如何提高无杂散动态范围(SpuriousFree Dynamic Range,SFDR)。
1 NCOs的工作原理
NCOs主要包括一个正弦波样点查找表(LUTs)和一个产生地址的累加器,如图1所示。

图1中n为累加器产生的地址位数,则LUTs有N=2n个输入。LUTs的输出分辨率/精度为L位(该参数与n有关),其工作原理见图2。

由图2可以看出,累加器产生地址码,循环从LUTs地址中取数正弦波的样点数据,其取数的速率越快,即步长μ越大,则产生的正弦波频率越高。
设步长参数μ由式(1)决定:

式中:N为LUTs的样点数据总量;fs为系统采样频率;fd为期望的正弦波的频率。
例如,累加器地址数据线宽度为8 b,则对应的LUTs的数据样点数为N=2n=256。如果采样频率为10 MHz,期望频率为2.5 MHz,则步长为:
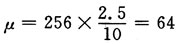
2 提高NCOs的无杂散动态范围
SFDR是无线系统设计中需要考虑的重要参数。如果振荡器产生的信号包含过多的杂波(Spurs)频率,这些干扰成分会使信号混频的质量变差,特别是当杂波频率接近中心频率时,在后续的电路中很难去除。
2.1 相位截断对频谱纯度的影响
当LUT输出正弦波样点数据时,只有整数部分可以用于输出,而小数部分则被忽略,这导致输出相位部分有截断。相位截断(Phase Truncation)的情况决定了产生的正弦波的纯度。如:当采样频率为100 kHz时,NCOs输出的期望频率为24.3 kHz,其NCOs设置参数见表1。从表1中可以看出,LUTs的分辨率为32 b,则可以忽略幅度值量化的影响,而杂波主要是由相位截断产生的。

2.2 幅度值量化对频谱纯度的影响
将LUT的深度增大为12 b(4 096),则可以忽略相位舍去对频谱纯度的影响,而杂波主要由幅度值的量化(Amplitude Quantization)产生。同样,当采样频率为100 kHz时,NCOs输出的期望频率24.3 kHz,NCOs设置参数见表2。

由图3,图4可以看出,相位截断产生的杂波远大于幅度值量化产生的杂波,是杂波的主要来源。
由以上的仿真波形可以看出,提高整数位的位数,虽然可以使相位截断小,频率杂波少,但要使用较大的LUTs容量。如整数位增加一位,即由n位增加n+1位,则LUTs的数据量会增加一倍。
提高小数位的位数可以有较高的步长精度和频率分辨率,但需要更加多的累加器。如小数部分由b位增加到b+1位,虽然对LUTs无影响,但将累加器的加法器和延迟器分别增加1位,从而影响NCOs的输出频率。
提高LUTs输出分辨率对正弦波样点的幅度值量化影响小,但需要更多的LUTs存储器。如LUTs输出分辨率增加1位,由L位增加L+1 位,LUTs所需的存储容量扩大2n。
可见,采用传统的设计方法要达到无相位截断,则需要LUT的字长非常长,占用资源非常大,导致NCOs的成本很高,而这在实际实现过程中是不可行的。
2.3 相位加抖提高SFDR
通过以上的仿真研究可看出,虽然可以通过增加整数位和提高LUTs输出分辨率的方法来提高SFDR,但因它们要占用大量的资源,因而不是经济有效的方法。为有效解决杂波问题,必须考虑其他有效的方法。目前的主要技术手段有:
幅度加抖(Amplitude Dithering):在LUT的输出中加入低水平的噪声,以打散原有幅度值量化的噪声结构。
相位加抖(Phase Dithering):在累加器的输出中加入低水平的噪声,以打散原有相位截断的噪声结构。
带通滤波(Bandpass Filtering):在振荡器输出端加滤波器滤出毛刺频率。但该方法很难滤出靠近中心频率的杂波。
以上的仿真已经证明,相位截断对SFDR的影响量是最大的,是提高SFDR的首选方法。
相位加抖的数学模型如图5所示。在LUTs地址字截断之前,在累加器的输出中加入低水平的伪随机噪声(A Low-level of Pseudo Random Noise),其中抖动的位数d是可变的。

抖动(Dither)可以通过线性反馈移位寄存器(Linear Feedback Shift Register,LFSR)来实现,见图6。LFSR有带M个抽头的移位寄存器,抽头反馈通常由或门构成,以产生一个周期为2M-1的序列。因此,长伪随机噪声序列(Long Pseudo Random Noise Sequences)可以用很少的硬件资源实现。例如,一个由12个元件构成的LFSR能够生成周期为4 095的PN序列。LFSR可以由M个D触发器和很少的组合器件构成。
来自某位的抽头,可以组合为一个矢量生成该位的抖动。实际实现时,可以采用较长的移位寄存器。移位寄存器越长,则输出的抖动越接近随机的性质。
下面分析相位加抖数据位数d对SFDR的影响。图7~图9分别为d=b-3,b+3,b三种情况的仿真波形,其中b为累加器控制字小数部分的位数。
加抖位数d=6-3时,仅对整数位产生0~1/8的影响。此时将SFDR提高了1 dB。可见,增加过少位数的抖动,仅对相位的截断有很小的影响,对改变杂波极为有限。
加抖位数d=b+3时,可以对整数位产生0~8的影响。此时将SFDR提高了9 dB。但同时可以看到,由于增加抖动的位数过多,虽然消除了杂波,但同时也提高了整个频谱的噪声电平。
加抖位数d=b时,可以对整个整数位产生0~1影响。此时将SFDR提高到106 dB。同时可以看到,由于增加抖动的位数恰当,既消除了杂波,又提高了整个频谱的噪声电平。
在用FPGA实现NCOs时,通过相位加噪可以提高整个输出频率的SFDR性能。但从图3,图6比较可以看出,在整个电路中串入了加法器,且关键路径包含了两个部分Dithering和NCOs的加法器,因而限制了整个设计的最大时钟频率。
振荡器 无线电 DSP 数字电视 GPS 滤波器 仿真 电路 Linear FPGA 相关文章:
- 数字下变频的FPGA实现(05-12)
- 基于FPGA的任意时延伪码序列产生方法(04-12)
- 在嵌入式设计中降低CPLD的功耗(04-30)
- Actel数模结合FPGA的远程控制器设计(05-13)
- 基于FPGA的相检宽带测频系统的设计(06-08)
- ACEX 1K系列CPLD配置方法探讨(06-09)
