基于单片机SRAM工艺的FPGA加密应用

在现代电子系统设计中，由于可编程逻辑器件的卓越性能、灵活方便的可升级特性，而得到了广泛的应用。由于大规模高密度可编程逻辑器件多采用SRAM工艺，要求每次上电，对FPGA器件进行重配置，这就使得可以通过监视配置的位数据流，进行克隆设计。因此，在关键、核心设备中，必须采用加密技术保护设计者的知识产权。

1　基于SRAM工艺FPGA的保密性问题

通常，采用SRAM工艺的FPGA芯片的的配置方法主要有三种：由计算机通过下载电缆配置、用专用配置芯片（如Altera公司的EPCX系列芯片）配置、采用存储器加微控制器的方法配置。第一种方法适合调试设计时要用，第二种和第三种在实际产品中使用较多。第二种方法的优点在于外围电路非常简单，体积较小，适用于不需要频繁升级的产品；第三种方法的优点在于成本较低，升级性能好。

以上几种方法在系统加电时，都需要将配置的比特流数据按照确定的时序写入SRAM工艺的FPGA。因此，采用一定的电路对配置FPGA的数据引脚进行采样，即可得到配置数据流信息。利用记录下来的配置数据可对另一块FPGA芯片进行配置，就实现了对FPGA内部设计电路的克隆。典型的克隆方法见图1。


  
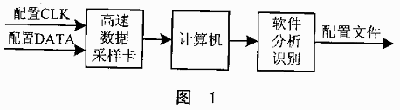
2 对SRAM工艺FPGA进行有效加密的方法

由于SRAM工艺的FPGA上电时的配置数据是可以被复制的，因此单独的一块FPGA芯片是无法实现有效加密的。FPGA芯片供应商对位数据流的定义是不公开的，因此无法通过外部的配置数据流信息推测内部电路。也就是说，通过对FPGA配置引脚的数据进行采样可得到配置信息。但也不能知道内部电路结构。如果在配置完成后使FPGA处于非工作状态，利用另外一块保密性较强的CPU产生密码验证信息与FPGA进行通信，仅在验证成功的情况下使能FPGA正常工作，则能有效地对设计进行加密。具体电路结构见图2。  


  
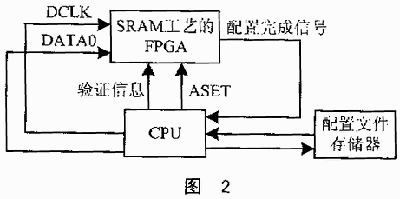
系统加电时，由单片机对SRAM工艺的FPGA进行配置。配置完成时，FPGA内部功能块的使能端为低，不能正常工作。此时，单片机判断到配置完成后，将ASET信号置为高电平，使能FPGA内的伪码发生电路工作；同时，单片机产生一个伪码验证信息，在FPGA中将两路伪码进行比较，两者完全匹配时，FPGA内部电路正常工作，否则不能正常工作。加密电路主要利用了配置完成后处于空闲状态的单片机和FPGA内部分逻辑单元，没有增加硬件成本。

由上述讨论可知，系统的加密能力主要由CPU的加密能力决定。这就要求CPU的加密算法要足够复杂，使得对验证信息的捕获与识别足够困难。最常见的加密算法就是产生两个伪随机序列发生器：一个位于SRAM工艺的FPGA内；另一个位于CPU内。当两者匹配时，通过验斑点。对PN码有两点要求：一方面，要求伪随机序列的长度足够长，使得要捕获整个序列不太可能；另一方面，伪随机序列的线性复杂度要足够高，使推测伪随机序列的结构不易实现。

通常采用的伪随机码发生器的反馈电路如图3所示。实际中，可采用级数较高的线性反馈移位寄存器来产生伪随机码。如采用40级线性移位寄存器产生的最大序列的周期为2?40=10?12。若将所有伪随机码截获并存储，就需要1000Gb的存储空间；若码速率为50Kbps，捕获时间将长达5555小时；当增加移位寄存器的级数时，所需的存储空间和捕获时间都会呈指数增长，以至于难以实现。采用较为简单的线性反馈电路被推测出反馈结构的可能性较大，因此实际的系统中，除了级数要较多之外，往往通过对多个线性移位寄存器产生的伪码进行特定运算产生长码，以增加所产生伪码的线性复杂度。  


  
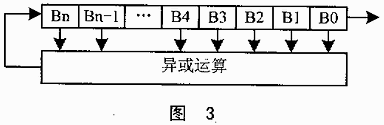
3　FPGA内的校验工作电路

在此采用40级线性反馈移位寄存器来产生伪随机码，特征多项式为20000012000005（八进制表示）。其移位寄存器表示形式为：Bin=B23?XOR?B21XORB2XORB0，FPGA内工作电路见图4。
  
  
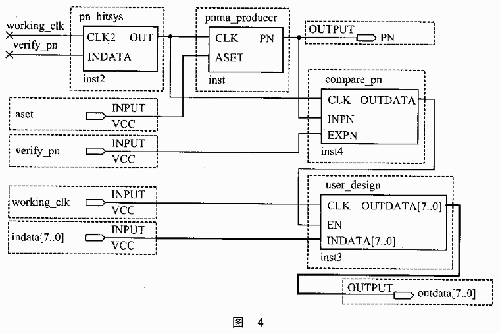
在上电之后，单片机将图4中的电路配置在FPGA中。配置完成后，单片机发送的ASET信号由低电平跳变为高电平，使得FPGA内的PN码产生电路开始工作，并于CPU发送过来的PN码进行比较。比较结果一致就使能USER_DESIGN模块正常工作。其中PLL_BITSYS模块用来发生VERIFY_PN的位同步时钟，采用微分锁相原理实现。各种参考资料都有较多介绍，在此不再详述。

COMPARE_PN模块完成对单片机发送的伪随机码和PNMA_PRODUCER模块产生的伪随机码的比较：当两路相同，输出1，不同时输出0；若两路伪码完全匹配，则恒定输出1，使USER_DESIGN电路正常工作，否则，输出为类似于伪码的信号，使USER_DESIGN电路不能正常工作。
  
4FPGA内的伪随机码