超高频RFID定位的相位式测距方法研究

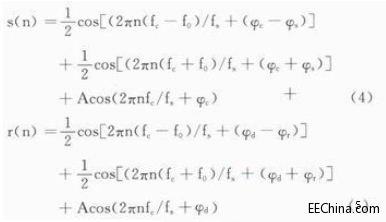
式(4)、式(5)所示的离散信号经FFT后自身带有相位信息，但是，在相位提取时，由非整周期的时域截断导致的频谱泄漏和多频率谐波信号各频率成分相互的干涉现象都会使相位偏离真实值，这就需要借助离散频谱校正技术。这里，综合考虑对主辦的能量集中性和窗函数表达式的复杂性，选用加hanning窗的比值法、能量重心法对相位进行提取与校正。

由式(4)、式(5)可知，射频载波信号经副载波调制后会产生一个差频项和一个和频项，它们的相位值分别对应载波相位与副载波相位的差与和，则副载波信号经标签反向散射返回后的相位差为

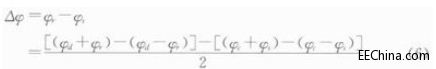
将式(6)带入式(1)，即可得到阅读器与标签之间的距离信息。

3 定位仿真分析

使用Matlab软件进行仿真，参数设置如下：

①信号参数，采样频率fs=9.128 MHz，副载波频率f0=2 MHz，载波频率fc=915 MHz，调制电平A=1。

②环境参数，在20 m×20 m二维空间的四个角上布置4个阅读器，标签位置随机投放。

③噪声，实际定位中噪声不可忽略，定义叠加噪声幅度，分别在SNR=5 dB、8 dB、11dB、14 dB、17 dB下仿真。

进行1000次蒙特卡洛仿真实验，定义均方根误差(RMSE)，式中n为测量次数，di为测量值与真实值的偏差。

把用比值法、能量重心法得到的测量值进行比较，如图4所示，在小信噪比环境下，比值法稍优于能量重心法，随着信噪比的增大，两种方法的测相误差和测距误差都随之减小，在SNR>11 dB后，两种算法的误差基本相同。在各信噪比下，测相误差最大达到6.27°，最小仅为1.43°，测距误差的范围为0.30～1.31 m。

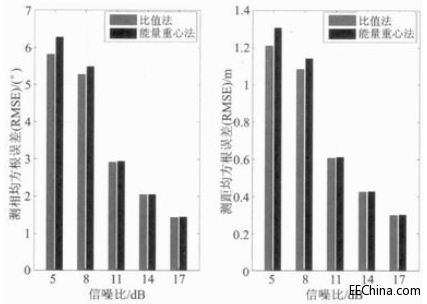
图4 测相，测距误差对比

图5为采用最小二乘法进行定位后两种算法的RMSE对比图。从整体趋势上来看，随着信噪比的增大，定位误差不断减小。在噪声较小SNR =17 dB时，两种方法RMSE均在0.35 m左右;在噪声增大到SNR=5 dB时，比值法RMSE为1.47 m，能量重心法RMSE为1.57 m。在SNR由5 dB增大到8 dB的过程中，两种方法的RMSE都有明显的降低，分别降低了0.43 m和0.51 m。

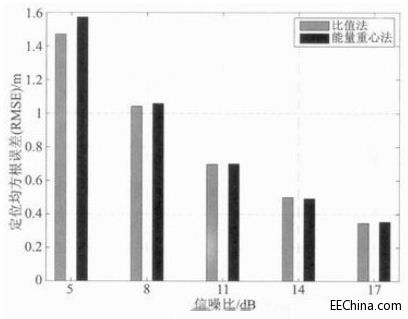
图5 定位误差对比

图6为在不同信噪比下，比值法的累计定位误差曲线图。在SNR≥14 dB时，定位较为准确，曲线收敛速度很快;在SNR=11 dB时，定位误差在0.94 m以下的概率为80%，定位准确度也很高;当信噪比减小到SNR=8 dB时，定位误差有86.8%的概率小于1.5 m;在SNR=5 dB时，定位误差小于1.5 m的概率为68%，但是可以看出曲线的收敛速度较慢。

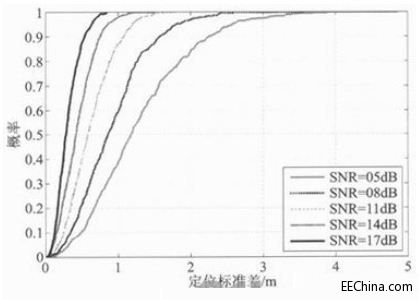
图6 信噪比定位误差的影响

结语

本文研究了一种用于超高频RFID定位的相位式测距方法，在带通采样方式下，结合离散频谱校正相位估计，进行了定位仿真。仿真实验中，测试了不同环境噪声对定位精度的影响。在噪声较大时，比值法的定位精度稍优于能量重心法;在小噪声环境下，两种方法定位精度差别不大，而能量重心法与比值法相比更为简单，较为适用。综上所述，基于相位法的定位有较好的有效性和稳定性，具有良好的应用前景。