一种自适应逆变电源的设计与实现

　　闭环调节脉宽调制（PWM）的逆变电源在各种类型的交流供电系统中得到了广泛的应用，例如：不间断电源（UPS），电压调节器（AVR），可编程交流电源（PAS）等。在这些系统中，要求能在瞬时或周期性的负载变动下，输出低谐波含量的波形。许多研究方案利用瞬时反馈控制技术，如：瞬时电压电流跟踪法、无差拍控制法、状态反馈控制法，获得了较好的动态响应。但是这类方法只能使系统对于瞬时的负载变化有较好的调节能力，而对周期性的负载变动所产生的周期性谐波抑制能力则很差。因此，这类系统对于非线性负载，如整流性负载，其输出总谐波含量仍然很高。另外，上述几种瞬时反馈控制的方法，从自身控制原理上讲仍存在不足之处，也妨碍了它们的进一步推广应用。其中，瞬时电压电流跟踪法，即所谓两态（或三态）滞环控制（Delta- PWM），电路的开关频率较高，且随精度要求的提高而提高，而且开关频率随其跟随的输出幅值变化而变化，谐波成分随机分布，输出频谱的分析较为困难，也不利于输出滤波器的设计。状态反馈控制的设计基于系统的精确数学模型，并要求状态反馈增益进行优化设计以增加系统的鲁棒性，而这两方面的误差都可能很大，从而降低了系统的性能。至于无差拍控制，由于其原理是基于电路计算的方法，因而对电路中元件参数的变化非常敏感，这对于负载经常变动的应用场合更不适用。虽然有的文献也提出了改进的方案，如添加负载参数辨识器，但效果仍然不理想。

　　PWM逆变电源性能的好坏最终取决于控制策略的优劣。自适应控制作为一种现代控制的方法，适用于系统数学模型未知，或者运行过程中会发生变化的情况，这无疑为解决逆变电源因负载变化而产生波形畸变的问题提供了一条思路。笔者正在基于DSP和单片机196的硬件基础上对该种自适应逆变电源进行深入的研究，它能自动地消除由于未知的负载周期性扰动所产生的交流周期畸变，大大提高了电源的品质。

　　2工作原理

　　见图1，在该系统中，将逆变桥、LC滤波器及整流性RC负载的整体作为系统的控制对象。其中，Ud

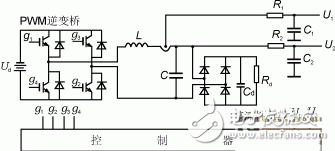
　　图1自适应PWM逆变电源硬件结构图

　　为直流电源电压，g1，g2，g3，g4为功率管开关信号，U1，U2分别为电流、电压反馈信号。该自适应控制方案由图2表示。

　　其中：r（k）—参考信号;

　　y（k）—系统输出;

　　e（k）—误差信号;

　　Q（z-1）、S（k，z-1）—辅助补偿器;

　　rc（k）—经补偿后的参考信号;

　　P（k，z-1）—系统受控对象的闭环传递函数。

　　该控制系统主要包括两个部分：其一为离散重复控制器，另一为自适应参数调节器。它们的工作原理如下：

　　（1）离散重复控制器

　　重复控制是指能消除所有包含在稳定闭环内的周期性误差的控制方案，如图3所示。

　　其中，P（z-1）代表被控对象的传函，d（k）为*信号，其余信号的定义与图2中相同。

　　由图可得：

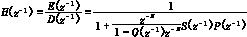
　　E（z-1）和D（z-1）为e（k），d（k）的Z变换，若d（k）是一个周期为N的扰动，则其Fourier变换为

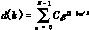
　　|Cn|代表Fourier系数

　　而传函在频域内可表示为

　　若Q（z-1）=1且P（z-1）是稳定的，则

　　|H（jω）|=0（ω=2nπ/N，n=0，…，N-1）

　　这表明这些周期性误差能被重复控制器所消除，在这种情况下就能获得无误差的跟随。但是，这就要求有很强的稳定度。在实际应用中，可以减弱这一条件，如令：

　　|H（jω）|《μ （jω ） （ ω="2nπ" /N， n="0，" 。..， N- 1）

　　这里μ（jω）为周期性误差的允许范围。

　　（2）自适应参数调节器

　　在重复控制系统的基础上添加自适应参数调节器，就构成自适应重复控制系统。自适应参数调节器从本质上讲是一种算法，它使系统具有自适应能力，能根据实际的系统特性调整控制参数，以达到所期望的性能指标。在本系统中，自适应参数调节器利用递推最小二乘算法（RLSE），实时辨识系统受控对象的结构参数，从而依据期望的性能指标对离散重复控制器的参数进行调节。

　　如图2，在本控制方案中，首先构成以图1中信号U1，U2为反馈的闭环，将该闭环的传函记为P（z-1），并近似认为其为二阶时变结构，即

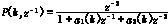
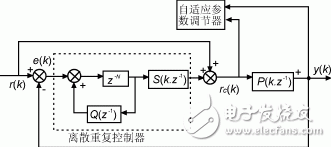
　　图2自适应重复控制系统控制框图

式中a1，a2为时变参数，其控制思想是：首先由自适应参数调节器在线地辨识系统受控对象的结构参数a1（k），a2（k），然后根据辨识结果调节辅助补偿器S（k，z-1）的参数，以得到适应系统结构的控制规律，从而使y（k）跟随r（k）。由于辨识是实时的，就能使系统总能根据实际的运行条件进行控制