基于MEMS加速度计的振动监控解决方案

简介

MEMS加速度计终于达到了能够测量广泛机器平台振动的阶段。其最近的能力进步，加上MEMS加速度计已有的相对于传统振动传感器的诸多优势（尺寸、重量、成本、抗冲击性、易用性），促使一类新兴的状态监控（CBM）系统开始使用MEMS加速度计。结果，许多CBM系统架构师、开发者甚至其客户首次考虑使用此类传感器。他们面临的问题常常是如何快速了解评估MEMS加速度计功能的方法，以便在其机器平台上测量最重要的振动特性。这初看起来似乎很困难，因为MEMS加速度计数据手册表述最重要性能特性的方式常常不是开发人员所熟悉的。例如，许多人熟悉用线速度（mm/s）来量化振动，但大多数MEMS加速度计数据手册是用基于重力的加速度（g）来表达其性能指标。幸运的是，有一些简单的技术可用来将加速度转换为速度，以及估计加速度计关键特性（频率响应、测量范围、噪声密度）对重要系统级标准（带宽、平坦度、峰值振动、分辨率）的影响。

基本振动特性

先从惯性运动角度考察线性振动。在此背景下，振动是平均位移为零的机械振荡。对于那些不希望其机器穿越整个车间的人来说，零平均位移非常重要！振动检测节点中核心传感器的价值与它反映机器振动最重要特性的能力高低直接相关。要评估特定MEMS加速度计在这方面的能力，首先必须从惯性运动角度对振动有一个基本了解。图1是振动情况的物理示意图，灰色部分表示中点，蓝色部分表示一个方向的峰值位移，红色部分表示另一方向的峰值位移。等式1提供了一个描述矩形物体瞬时加速度的数学模型，其振动频率为（fV），幅度为Arms。

图1.简单线性振动

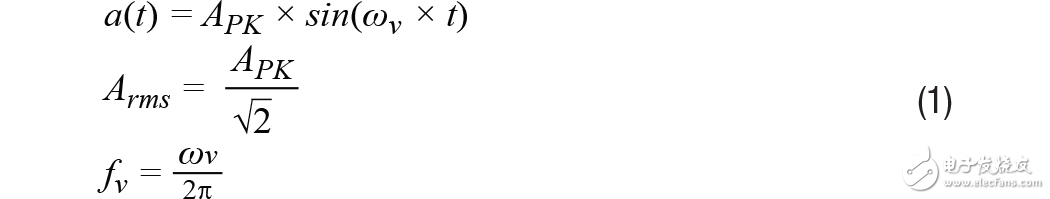
在大部分CBM应用中，机器平台的振动常常有比等式1所示模型更复杂的频谱特征，但此模型为学习发现之旅提供了一个很好的出发点，因为它给出了CBM系统常常会跟踪的两个常见振动特性：幅度和频率。此方法对关键特性到线性速度项的转换也很有用（稍后将有更多说明）。图2提供了两类不同振动模式的频谱视图。第一类（参见图2中的蓝线）在其频率范围（f1到f6）内具有恒定幅度。第二类（参见图2中的红线）在四个不同频率处出现了峰值幅度：f2， f3， f4， 和 f5.

图2.CM振动模式示例

系统要求

测量范围、频率范围（带宽）和分辨率是用来量化振动检测节点能力的三个常见特性。图2通过虚线矩形框显示了这些特性，其边界分别对应最低频率（fMIN）、最高频率（fMAX）、最小幅度（AMIN）和最大幅度（AMAX）。当考虑将MEMS加速度计用作振动检测节点中的核心传感器时，系统架构师很可能想在设计早期分析其频率响应、测量范围和噪声行为。有一些简单的技术可用来评估加速度计的各种特性，进而预判其是否满足指定的一组要求。很显然，系统架构师最终必须通过实际验证和鉴定来核验上述估计，但由对加速度计能力的早期分析和预测所得来的期望对这些工作是有价值的。

频率响应

图2提供了一个简单的一阶模型，其描述了时域中MEMS加速度计对线性加速度（a）的响应（y）。在该关系中，偏置（b）表示传感器无振动时的输出值。比例因子（KA）表示MEMS加速度计响应（y）相对于线性加速度（a）变化的改变量。

传感器的频率响应描述比例因子（KA）相对于频率的值。在MEMS加速度计中，频率响应主要有两个贡献因素：（1） 其机械结构的响应；（2） 其信号链中的滤波响应。等式3提供了一个通用二阶模型，其近似描述了MEMS加速度计机械部分对频率的响应。在该模型中，fO表示谐振频率，Q表示品质因数。

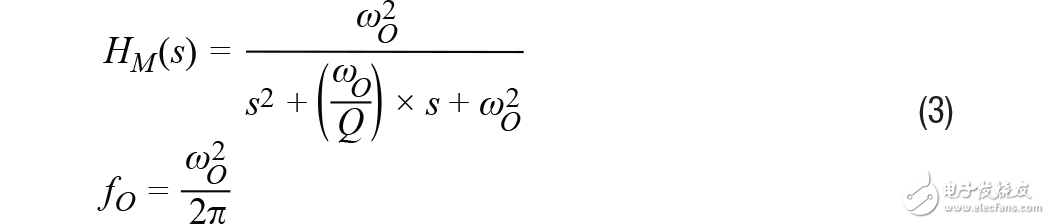
信号链的贡献常常取决于应用所需的滤波。某些MEMS加速度计使用单极点低通滤波器来帮助降低谐振频率时的响应增益。等式4为此类滤波器相关的频率响应（HSC）提供了一个通用模型。在该类滤波器模型中，截止频率（fC）表示输出信号幅度比输入信号低√2倍时的频率。

等式5将机械结构（HM）和信号链（HSC）的贡献进行了合并。

图3直接应用此模型来预测ADXL356（x轴）的频率响应。此模型假设标称谐振频率为5500 Hz，Q为17，使用截止频为1500 Hz的单极点低通滤波器。注意，等式5和等式4仅描述了传感器的响应。此模型未考虑加速度计与其监控的平台的耦合方式。

图3.ADXL356频率响应

带宽与平坦度的关系

在利用单极点低通滤波器（例如等式4所用）建立频率响应的信号链中，其带宽规格常常说明了其输出信号提供输入信号50%功率时的频率。对于更复杂的响应，例如等式5和等式3中的三阶模型，带宽规格常常带有相应的平坦度规格。平坦度特性描述比率因子在频率范围（