精通信号处理设计小Tips（8）：检测淹没在噪声中的信号

　　本文作者maxfiner，毕业于西安电子科技大学，拥有信号与信息处理专业硕士学位。maxfiner曾供职于华为通信技术公司无线通信部门，拥有多年的工程项目研发经验，同时兼备算法理论研究，仿真验证，以及对应的硬件设计实现能力；具备通信物理层开发设计各个方面的实战经验...

　　相关函数的应用很广，比如噪声中信号的检测，信号中隐含周期性的检测，信号时延长度的测量等等。这一节专门讨论利用自相关函数检测淹没在噪声下的周期性信号。

　　一个信号，由于噪声的影响，从波形上看，已经面目全非，杂乱不堪。如下图所示：

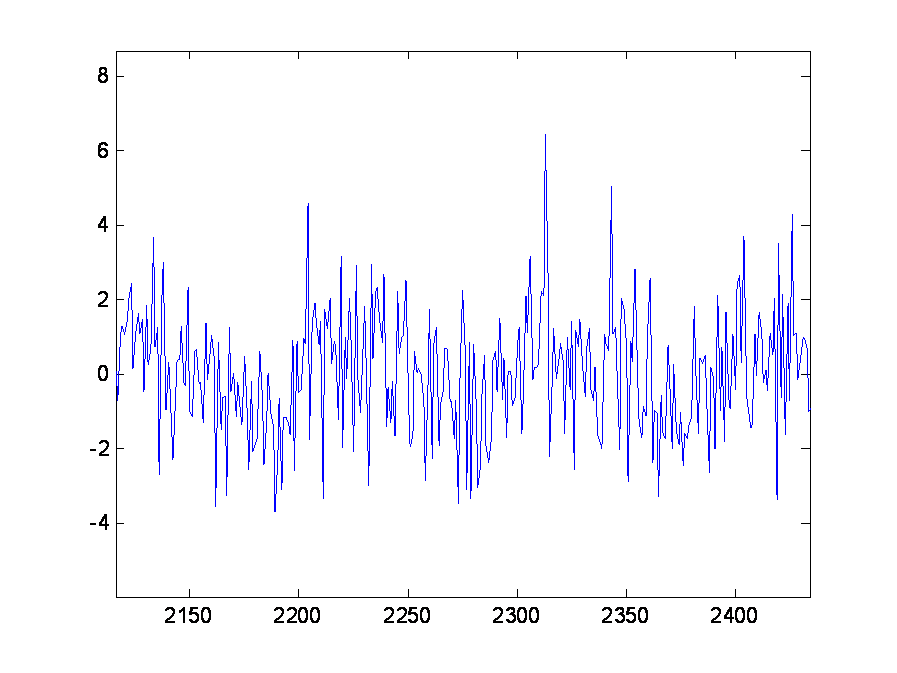
　　基于信号的自相关累积可以检测是否有周期信号的存在，这是基于几个前提：

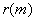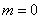　　第一，通常把噪声都看作加性的白噪声对待，因为这种噪声从理论上便于分析和处理。而白噪声的自相关函数有着非常独特的个性，就是自相关函数只在时有一定的数值，在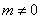则为零值。这是白噪声本身的完全随机性决定的。也正是基于这个性质，我们才有可能从强噪声背景中提取出我们感兴趣的信号。

　　第二，周期信号的自相关函数，仍是周期函数，并且周期和原函数周期相同。这从自相关函数的定义可以很容易推导出来。

　　第三，白噪声和周期信号完全不相关，白噪声的完全随机性导致它和任何函数都不相关恋。它们之间的互相关函数可认为是零。这是很多理论推导的一个前提。

　　基于自相关函数的定义，我们可以从公式上做一下简单的推导，看看添加了噪声后的信号的自相关函数到底是什么样子。假定我们的信号为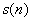，白噪声信号为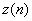，则添加了白噪声的信号为。

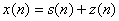　　那么，基于上面的三个前提，我们可以把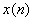的自相关函数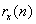表示成如下的形式。公式推导看上去很麻烦，其实一步一步都有严格的规律和理由，认真观察和分析，可以增进对自相关函数和互相关函数的理解，也可以加强公式推导的基础能力。

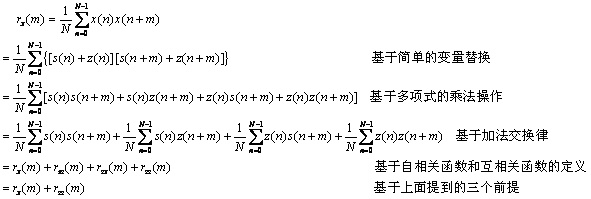
也就是说，

　　理论公式非常严密但不直观。还是找个实际例子验证下吧。构造一个正弦波周期信号和白噪声信号，看看它们叠加后的信号的自相关函数到底是个什么样子。

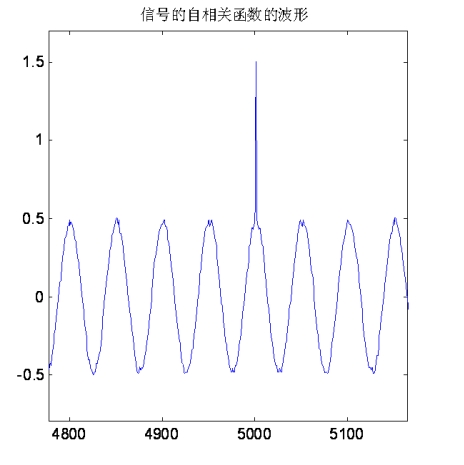
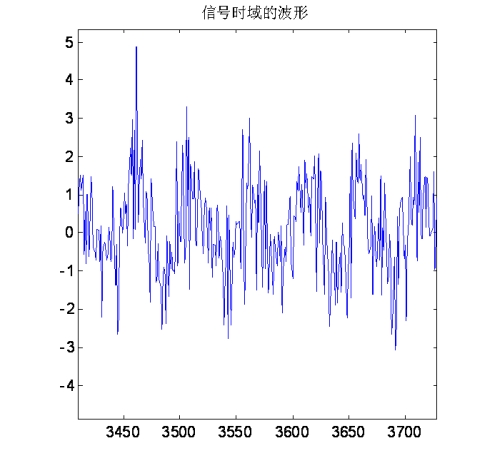
　　自相关函数在0位置是一个相对较大的数值，这是白噪声自身相关累积导致的。在非零位置，则完全由周期信号来决定了。

　　相应的matlab仿真验证代码如下，

　　fs = 5e3;

　　n = 0:1/fs:1;

　　len = length（n）;

　　freq = 100;

　　s = sin（2*pi*freq*n）;

　　n = randn（1，len）;

　　x = s + n;

　　rr = xcorr（x，‘unbiased’）;

　　figure，subplot（121），plot（x）;TItle（‘ÐźÅʱÓòµÄ²¨ÐÎ’）;

　　subplot（122），plot（rr）;TItle（‘ÐźŵÄ&TImes;ÔÏà¹Øº¯ÊýµÄ²¨ÐÎ’）;

　　值得说明的是，相关函数采用matlab工具箱提供的函数xcorr，它有两种计算方式，一种叫"biased"，即有偏的。一种叫"unbiased"，即无偏的。这是由于实际计算相关函数时，实际数据的长度总是有限的，那么随着相关函数中m的增大，相关累积求和的样点数是逐渐减小的，当采用上面提到的自相关函数计算公式时，统一都除以N，导致相关函数随着m的增大会线性减，这就是有偏的计算方式，意思是计算值的统计上的均值和实际值之间并不一致，存在一定的偏差。这种计算方式导致当m的绝对值接近实际采集信号长度N时，误差会变得越来越大。若是把m的增大导致累积样点减少这个因素考虑进去，不再统一除以N，而是除以N-m，则相关函数不再会产生线性减小的问题，这就对应代码中的无偏的计算方式。
 

下期开讲——精通信号处理设计小TIps（9）：估算信号在模拟通道的延时，敬请关注！
声明：电子发烧友网版权所有，谢绝转载！