传输系统中的时钟同步技术
时间:02-11
来源:不详
点击:
同步模块是每个系统的心脏,它为系统中的其他每个模块馈送正确的时钟信号。因此需要对同步模块的设计和实现给予特别关注。本文对影响系统设计的时钟特性进行了考察,并对信号恶化的原因进行了评估。本文还分析了同步恶化的影响,并对标准化组织为确保传输质量和各种传输设备的互操作性而制定的标准要求进行了探讨。
摘要:
网络同步和时钟产生是高速传输系统设计的重要方面。为了通过降低发射和接收错误来提高网络效率,必须使系统的各个阶段都要使用的时钟的质量保持特定的等级。网络标准定义同步网络的体系结构及其在标准接口上的预期性能,以保证传输质量和传输设备的无缝集成。有大量的同步问题,系统设计人员在建立系统体系结构时必须十分清楚。本文论述了时钟恶化的各种来源,如抖动和漂移。本文还讨论了传输系统中时钟恶化的原因和影响,并分析了标准要求,提出了各种实现技巧。
基本概念:抖动和漂移
抖动的一般定义可以是"一个事件对其理想出现的短暂偏离"。在数字传输系统中,抖动被定义为数字信号的重要时刻在时间上偏离其理想位置的短暂变动。重要时刻可以是一个周期为 T1 的位流的最佳采样时刻。虽然希望各个位在 T 的整数倍位置出现,但实际上会有所不同。这种脉冲位置调制被认为是一种抖动。这也被称为数字信号的相位噪声。在下图中,实际信号边沿在理想信号边沿附近作周期性移动,演示了周期性抖动的概念。
抖动,不同于相位噪声,它以单位间隔 (UI) 为单位来表示。一个单位间隔相当于一个信号周期 (T),等于 360 度。假设事件为 E,第 n 次出现表示为 tE[n] 。则瞬时抖动可以表示为:
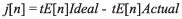
一组包括 N 个抖动测量的峰到峰抖动值使用最小和最大瞬时抖动测量计算如下:
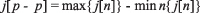
漂移是低频抖动。两者之间的典型划分点为 10 Hz。抖动和漂移所导致的影响会显现在传输系统的不同但特定的区域。
抖动类型
根据产生原因,抖动可分成两种主要类型:随机抖动和确定性抖动。随机抖动,正如其名,是不可预测的,由随机的噪声影响如热噪声等引起。随机抖动通常发生在数字信号的边沿转换期间,造成随机的区间交叉。毫无疑问,随机抖动具有高斯概率密度函数 (PDF),由其均值 (μ) 和均方根值 (rms) (σ) 决定。由于高斯函数的尾在均值的两侧无限延伸,瞬时抖动和峰到峰抖动可以是无限值。因此随机抖动通常采用其均方根值来表示和测量。
对抖动余量来讲,峰到峰抖动比均方根抖动更为有用,因此需要把随机抖动的均方根值转换成峰到峰值。为将均方根抖动转换成峰到峰抖动,定义了随机抖动高斯函数的任意极限 (arbitrary limit)。误码率 (BER) 是这种转换中的一个有用参数,其假设高斯函数中的瞬时抖动一旦落在其强制极限之外即出现误码。通过下面两个公式,就可以得到均方根抖动到峰到峰抖动的换算。3
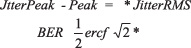
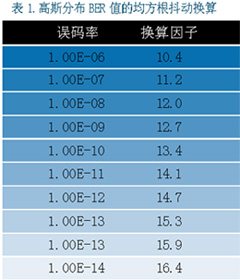
由公式可得到下表,表中峰到峰抖动对应不同的 BER 值。
确定性抖动是有界的,因此可以预测,且具有确定的幅度极限。考虑集成电路 (IC) 系统,有大量的工艺、器件和系统级因素将会影响确定性抖动。占空比失真 (DCD) 和脉冲宽度失真 (PWD) 会造成数字信号的失真,使过零区间偏离理想位置,向上或向下移动。这些失真通常是由信号的上升沿和下降沿之间时序不同而造成。如果非平衡系统中存在地电位漂移、差分输入之间存在电压偏移、信号的上升和下降时间出现变化等,也可能造成这种失真。
数据相关抖动 (DDJ) 和符号间干扰 (ISI) 致使信号具有不同的过零区间电平,导致每种唯一的位型出现不同的信号转换。这也称为模式相关抖动 (PDJ)。信号路径的低频截止点和高频带宽将影响 DDJ。当信号路径的带宽可与信号的带宽进行比较时,位就会延伸到相邻位时间内,造成符号间干扰 (ISI)。低频截止点会使低频器件的信号出现失真,而系统的高频带宽限制将使高频器件性能下降。7
正弦抖动以正弦模式调制信号边沿。这可能是由于供给整个系统的电源或者甚至系统中的其他振荡造成。接地反弹和其他电源变动也可能造成正弦抖动。正弦抖动广泛用于抖动环境的测试和仿真。不相关抖动可能由电源噪声或串扰和其他电磁干扰造成。
考虑抖动对数字信号的影响时,需要将整个确定性抖动和随机抖动考虑在内。确定性抖动和随机抖动的总计结果将产生另外一种概率分布4:双模响应,其中部表示确定性抖动,尾部为高斯响应,表示随机抖动分量。
摘要:
网络同步和时钟产生是高速传输系统设计的重要方面。为了通过降低发射和接收错误来提高网络效率,必须使系统的各个阶段都要使用的时钟的质量保持特定的等级。网络标准定义同步网络的体系结构及其在标准接口上的预期性能,以保证传输质量和传输设备的无缝集成。有大量的同步问题,系统设计人员在建立系统体系结构时必须十分清楚。本文论述了时钟恶化的各种来源,如抖动和漂移。本文还讨论了传输系统中时钟恶化的原因和影响,并分析了标准要求,提出了各种实现技巧。
基本概念:抖动和漂移
抖动的一般定义可以是"一个事件对其理想出现的短暂偏离"。在数字传输系统中,抖动被定义为数字信号的重要时刻在时间上偏离其理想位置的短暂变动。重要时刻可以是一个周期为 T1 的位流的最佳采样时刻。虽然希望各个位在 T 的整数倍位置出现,但实际上会有所不同。这种脉冲位置调制被认为是一种抖动。这也被称为数字信号的相位噪声。在下图中,实际信号边沿在理想信号边沿附近作周期性移动,演示了周期性抖动的概念。
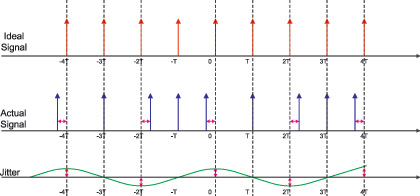
图 1.抖动示意
抖动,不同于相位噪声,它以单位间隔 (UI) 为单位来表示。一个单位间隔相当于一个信号周期 (T),等于 360 度。假设事件为 E,第 n 次出现表示为 tE[n] 。则瞬时抖动可以表示为:
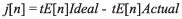
一组包括 N 个抖动测量的峰到峰抖动值使用最小和最大瞬时抖动测量计算如下:
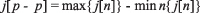
漂移是低频抖动。两者之间的典型划分点为 10 Hz。抖动和漂移所导致的影响会显现在传输系统的不同但特定的区域。
抖动类型
根据产生原因,抖动可分成两种主要类型:随机抖动和确定性抖动。随机抖动,正如其名,是不可预测的,由随机的噪声影响如热噪声等引起。随机抖动通常发生在数字信号的边沿转换期间,造成随机的区间交叉。毫无疑问,随机抖动具有高斯概率密度函数 (PDF),由其均值 (μ) 和均方根值 (rms) (σ) 决定。由于高斯函数的尾在均值的两侧无限延伸,瞬时抖动和峰到峰抖动可以是无限值。因此随机抖动通常采用其均方根值来表示和测量。
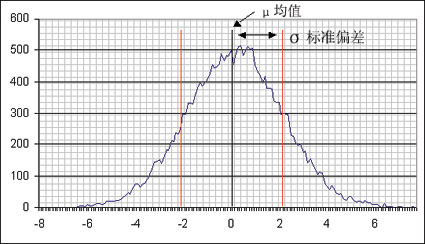
图 2.以高斯概率密度函数表示的随机抖动
对抖动余量来讲,峰到峰抖动比均方根抖动更为有用,因此需要把随机抖动的均方根值转换成峰到峰值。为将均方根抖动转换成峰到峰抖动,定义了随机抖动高斯函数的任意极限 (arbitrary limit)。误码率 (BER) 是这种转换中的一个有用参数,其假设高斯函数中的瞬时抖动一旦落在其强制极限之外即出现误码。通过下面两个公式,就可以得到均方根抖动到峰到峰抖动的换算。3
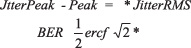
由公式可得到下表,表中峰到峰抖动对应不同的 BER 值。
确定性抖动是有界的,因此可以预测,且具有确定的幅度极限。考虑集成电路 (IC) 系统,有大量的工艺、器件和系统级因素将会影响确定性抖动。占空比失真 (DCD) 和脉冲宽度失真 (PWD) 会造成数字信号的失真,使过零区间偏离理想位置,向上或向下移动。这些失真通常是由信号的上升沿和下降沿之间时序不同而造成。如果非平衡系统中存在地电位漂移、差分输入之间存在电压偏移、信号的上升和下降时间出现变化等,也可能造成这种失真。
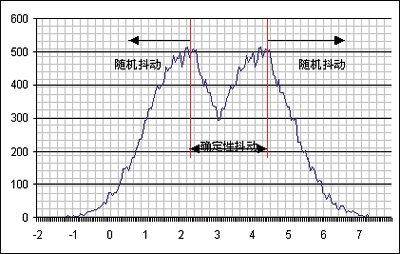
图 3,总抖动的双模表示
数据相关抖动 (DDJ) 和符号间干扰 (ISI) 致使信号具有不同的过零区间电平,导致每种唯一的位型出现不同的信号转换。这也称为模式相关抖动 (PDJ)。信号路径的低频截止点和高频带宽将影响 DDJ。当信号路径的带宽可与信号的带宽进行比较时,位就会延伸到相邻位时间内,造成符号间干扰 (ISI)。低频截止点会使低频器件的信号出现失真,而系统的高频带宽限制将使高频器件性能下降。7
正弦抖动以正弦模式调制信号边沿。这可能是由于供给整个系统的电源或者甚至系统中的其他振荡造成。接地反弹和其他电源变动也可能造成正弦抖动。正弦抖动广泛用于抖动环境的测试和仿真。不相关抖动可能由电源噪声或串扰和其他电磁干扰造成。
考虑抖动对数字信号的影响时,需要将整个确定性抖动和随机抖动考虑在内。确定性抖动和随机抖动的总计结果将产生另外一种概率分布4:双模响应,其中部表示确定性抖动,尾部为高斯响应,表示随机抖动分量。
- 推陈出新 时钟同步技术的现状及发展(02-11)
- 基于SNMP的电源设备管理无线传输系统的框架组成(11-17)
- 基于物联网的智能电网解决方案(06-22)
- LT3751如何使高压电容器充电变得简单(08-12)
- 三路输出LED驱动器可驱动共阳极LED串(08-17)
- 浪涌抑制器IC简化了危险环境中电子设备的本质安全势垒设计(08-19)
