基于PCI-9846H的死区时间引起的电压波形畸变的研究

　挑战

　　目前国内外基于电机模型建立的控制策略在电机的低速脉动、高速弱磁、稳定性和输出转矩一致性等方面还存在诸多问题。为了能更好的解决电机的低速转矩脉动的问题，本文建立了引入逆变器死区时间的电机模型，逆变器死区时间很短并且IGBT的开关过程还存在延时和滞后的问题，为了能够准确的捕捉死区时间引起的电压波形畸变，要求数据采集卡有很高的采样率，除此之外，为了使研究结果更加精确，需要板卡具有较高的信噪比以及有效位。综上所述，在死区时间引起的电压波形畸变的研究中，需要一块高采样率、高精度以及高信噪比的板卡以满足对信号捕捉的要求。

　　解决方案

　　首先对死区效应进行分析，针对仿真结果提出一种减小死区时间引起电压波形畸变的方法，通过应用具有16位高分辨率A/D转换器并且同步采样采样率高达16MS/s的数据采集卡PCI-9846H配合电流传感器、电压传感器、转矩仪、电机及其控制器、测功机等设备完成车用电机试验平台的搭建，通过凌华公司提供的LABVIEW相关驱动程序进行上位机数据采集系统的开发设计，通过对电压、电流、转矩、转速信息的采集与分析，对本文提出的减小死区时间对输出电压波形畸变的方法进行了验证，试验结果基于PCI-9846H的数据采集系统具有高采样率和高采样精度，能够满足本文对死区时间引起的电压波形畸变信号捕捉的要求，同时本文提出的改进方法，能够很好的改善电压的输出波形，进而能够减少死区时间对电机在低速工况时性能的影响

　　引言

　　电机驱动系统是电动汽车的核心部分［1-2］。按所使用电机的类型可以分为直流电机驱动系统和交流电机驱动系统［3］，而交流电机驱动系统中，感应电机容易被接受，使用较广泛，永磁同步电机由于其本身的高能量密度与高效率，具有比较大的竞争优势，应用范围日益增多。

　　为了满足整车动力性能要求，电机驱动系统要有较高的动态性能，目前比较成功的控制策略包括：基于稳态模型的变频变压控制（VVVF）、基于动态模型的磁场定向控制（FOC）以及直接转矩控制（Direct Torque Control——DTC）。其中直接转矩控制是在矢量控制基础之上发展起来的，其主要优点是：摒弃了矢量控制中的解耦思想，直接控制电动机的磁链和转矩，并利用定子磁链定向代替了矢量控制中的转子磁链定向，避开了电动机中不易确定的参数（转子电阻等）识别。目前国内外的永磁同步电机的数学模型只是基于中线不接出三相对称绕组条件下，引入转子磁链、定子漏抗、及各绕组的互感而建立的，忽略了轴承及其他杂散损耗以及PWM波等因素对电机的影响，因此基于该电机模型建立的控制策略在电机的低速脉动、高速弱磁、稳定性和输出转矩一致性等方面还存在诸多问题［5］。为了能更好的解决直接转矩控制下电机的低速转矩脉动的问题，本文建立了引入逆变器死区时间的电机模型，通过对死区时间的产生和作用机理进行分析，得出引起输出电压波形畸变以及相位变化的关键影响因子，针对仿真结果提出一种减小死区时间引起电压波形畸变的方法，通过应用PCI-9846H、电流传感器、电压传感器、转矩仪、电机及其控制器、测功机等设备完成车用电机试验平台的搭建，上位机通过LABVIEW编写数据采集系统，通过对电压、电流、转矩、转速信息的采集与分析，对本文提出的减小死区时间对输出电压波形畸变的方法进行了验证。

　　1.逆变器死区时间的研究

　　1.1逆变器死区时间产生机理

　　对于永磁同步电机驱动而言，在IGBT正常工作时，上下桥臂是交替互补导通的。在交替过程中必须存在上下桥臂同时关闭的状态，确保在上/下桥臂导通前，对应的互补下/上桥臂可靠关断，这段上下两个桥臂同时关断的时间称为死区时间。针对目前市场上IGBT的调研发现，逆变器死区时间一般为3～7μs［6］。在电机工作在一定转速以上时，由于基波电压足够大，死区效应对基波电压影响较小，所以不为人们所重视；但电机工作在低速时，基波电压很小，死区效应对基波电压影响相对较大，死区时间越长，逆变器输出电压的损耗越大，电压波形的畸变程度也会变大，除此之外死区时间还会影响输出电压的相位，使PWM波形不再对称于中心，造成电机损耗增加，效率降低，输出转矩脉动等。图1所示为死区时间产生的机理以及对输出电压的影响，其中V为理想的PWM电压输出波形，Ua-为负母线电

　　压，Ua+为正母线电压，v为误差电压，Ia为输出电流。

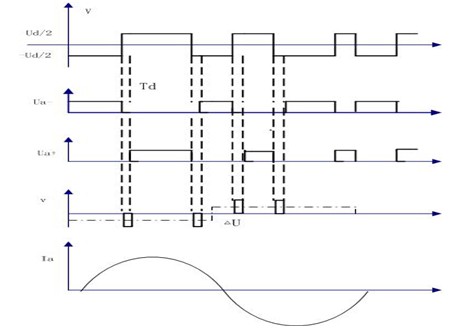
　　图1 死区效应

　　由图1所示，可以发现误差电压具有以下特征［7］：

　　1） 在每个开关周期内均存在一个误差电压脉冲；

2） 每个误差