数字形态学滤波器与智能车路径记忆

引言

　　"飞思卡尔"杯全国大学生智能车竞赛规则明确指出，智能车在赛道上连续跑两圈，并记录其中最好的单圈成绩，这使路径记忆算法成为可能。如图1所示，赛道记忆算法在第一圈以最安全的速度缓慢驶过一圈，并将赛道信息保存下来，第二圈根据保存下来的信息进行车速和转角决策的相应最优化，从而在第二圈取得好成绩。无论智能车的传感器前瞻距离有多远，在跑圈时它都只能预测在一段有限距离内赛道的情况。而采用赛道记忆算法的智能车，在第二圈时已对整个赛道有了全面的认识，从而在相同条件下，将比不使用赛道记忆的智能车更具优势。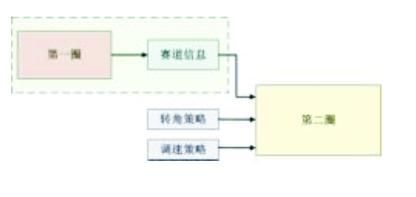

　　第一圈准确记忆赛道信息是第二圈控制策略的基础，是比赛成败的关键。但是在第一圈中不论控制策略如何优秀，赛车总会或多或少的偏离赛道，舵机的转角信息总会出现一定程度的毛刺和扰动等粗大误差，其幅值足以引起处理器的误判。如果不加处理直接应用于第二圈控制，会对赛车造成严重干扰，不能以极限速度跑完比赛或者冲出赛道。通常的处理方法有两种：一是通过阈值比较丢弃干扰值，但同时赛道信息也会同干扰信息一起被丢弃；二是通过低通滤波将干扰平均到多个位置，但同时破坏了赛道原始信息，而且在干扰幅值很大的时候效果也不是很明显。

　　数学形态学(Mathematical Morphology)是一种新型的数字图像处理方法和理论，其主要内容是设计一整套的变换(运算)、概念和算法，用以描述图像的基本特征。提供了非常有效的非线性滤波技术，该技术只取决于信号的局部形状特征。因此，它在诸如形状分析、模式识别、视觉校验、计算机视觉等方面，要比传统的线性滤波更为有效。

　　算法的选取与实验结果对比

　　数学形态学的运算以腐蚀和膨胀这两种基本运算为基础，引出了其它几个常用的数学形态运算。数学形态学中最常见的基本运算只有七种，分别为：腐蚀、膨胀、开运算、闭运算、击中、细化和粗化，它们是全部形态学的基础。它们的定义如下：

设X代表一个数字图像，我们假定该图像是二值的，即取值只有1或0，则X表示一个二进制信号集合，B是一个简单的紧集合，称为"结构元素"。X被B膨胀和腐蚀的结果可以分别定义为：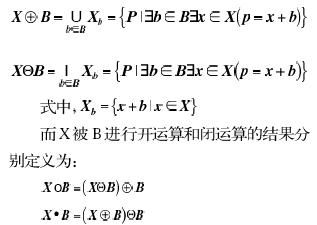

　　在数字图形处理领域中，数学形态学主要用于非线性变形，它可以局部地修改信号的几何特征，并提供有关信号的几何特征信息。根据不同的信号的形态特征，可以采用不同的数学形态学运算对信号进行处理，这些数学形态与运算都被视为数学形态滤波器。在这种应用方法中，每一个信号都被视为适当的维数的欧几里德空间中的集合。数学形态滤波器被定义为集合的运算，它使信号的图形变形，以提供关于其几何结构的数字化信息。对于被视为集合的二进制信号，腐蚀、膨胀、开运算和闭运算是最简单的形态运算。这些滤波器还可以引申到多维信号中去。此时，形态滤波器利用的是灰值图的数学形态运算的定义。下面将探讨如何将数学形态滤波器应用到舵机转角信号(一维数字信号)的处理中，实现去除脉冲噪声和减小扰动，以及在单片机上编程实现和快速运算的方法。

　　数学形态滤波器通常是用在二维图形的处理，为把数学形态滤波器推广到一维的信号的处理中，下面再介绍一下腐蚀、膨胀、开运算和闭运算这一个基本运算在一维信号处理中的定义：

　　设H、K分别为h[n]和k[n]的定义域，长度分别为N和M，一般N>M。H和K均为整数集合。

　　h[n]指包含舵机转角信号的数字化序列，k[n]指结构元素序列。

　　h被k腐蚀：

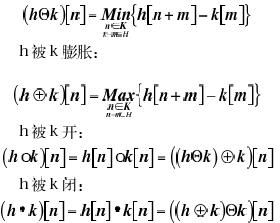
采用数字形态滤波方法，还要选用合理的算法。其中，如何选取模板序列的长度是关键，如果模板序列过长会将有用信号当作噪声滤除，过短则达不到滤除噪声的目的。在采样速率一定的情况下，序列的长度与时间成正比，这要求模板的长度要小于模型车的最小转弯时间，大于舵机扰动的最长时间。第一圈让模型车匀速通过，这样处理有两个优点：

　　1) 可以固定最小转弯时间，从而确定模板的长度。非匀速通过时速转弯时间不定，要求模板长度可变，从而造成后续处理复杂，稳定性不高。

　　2) 采样序列的顺序可以直接转化为位移量，便于后续控制策略处理。相对于非匀速通过速度与时间乘积得到的位移，直接转化得到的位移更准确(在标准的韩国赛道上，实验模型车直接转化得到的赛道长度误差小于5cm，速度与时间乘积得到赛道长度误差在10cm以上)。

实验系统在图2所示的赛道上，智能车对赛道信息的采样速率为200Hz，以1.5m/s的速度匀速跑完第一圈的数据如图3所示。可以看到在弯道中，舵机的转角信息存在着严重的毛刺和扰动，不能直接用于第二圈的控制策略。图4为matlab中采用3阶巴特沃兹滤波处理后的结果，干扰的