What is a reflection coefficient of this circuit?

Hello,

Can anyone help me understand what is a reflection coefficient of below circuit?
I'm certain that Γ2 is (ZL-Z2)/(ZL+Z2)
However what is Γ1 (reflection coefficient at Z=-l)? Is it (Zin-Z1)/(Zin+Z1) or Γ2*e^(-2jβl)?
Does Γ1 change if Z1 is replaced by a discrete resistor?

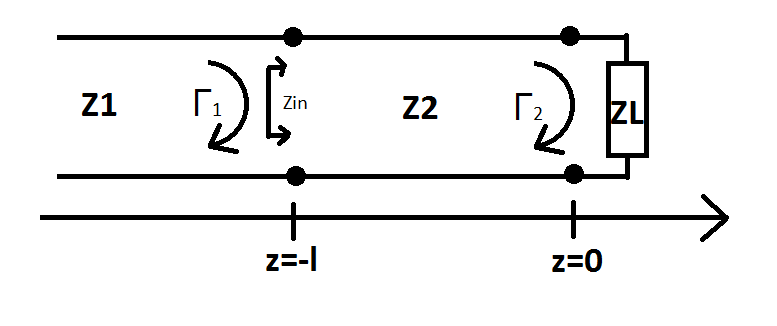
Its implied that Z2 is a transmission line by the change in z from 0 to -l across it.

Γ1 will depend on Γ2, and the properties of this transmission line. It will also depend on the mismatch between the line and the incident impedance Z1.

Lastly, Z1 is assumed to be infinitely long, due to the fact that the end is not shown. Therefore, Γ1 will not change if replaced with a discrete resistor.

Here is how you can calculate Zin from your Z2 and ZL (different names used in my equation, but you get the idea).

Having that, you can calculate Γ1 from Zin and Z1.

Thanks PlanarMetamaterials,
So if I understand correctly, you are implying that Γ1=(Zin-Z1)/(Zin+Z1) and it won't change whether Z1 is an infinitely long transmission line or a discrete resistor. Right?
But here's why I got confused.
I was studying myself using U of Kentucky's Prof. Jim Stiles's lecture note and from section 2.6, page 4~5, he defines Γ1 as Γ2*e^(-2jβl) which is just phase shifted Γ2 and is independent of Z1.
Below is a screenshot of his lecture note.

Why is that so?

Volker,

Could you explain why Γ1 is not Γ2*e^(-2jβl) but (Zin-Z1)/(Zin+Z1)

He has defined Γin as ΓL*e^(-2jβl). This merely the transformed expression of ΓL, and therefore does not take into account the mismatch between Zg and Zo (and therefore is not equal to Γ1). It appears, however, that he has accounted for this in his expression of Zo+.