温故而知新之二阶系统（中）

接上期，http://bbs.eetop.cn/thread-625164-1-1.html

这次我们从时域角度，回顾不同阻尼因子下二阶系统的冲激响应和阶跃响应，公式会比较多。

冲激响应

我们知道系统函数是系统对单位冲激响应的拉普拉斯变换，通过拉普拉斯反变换，就可以得到不同阻尼情况下的单位冲激响应了。

二阶系统的幅频响应如图1所示。两个根和阻尼因子有关。

图1

不同阻尼因子时，系统函数的根形式如图2所示。

图2

冲激响应时域表达式如图3所示。可以看到当0<ζ<1时，其瞬态响应包含了正弦项，也就是冲激响应存在振荡。

图3

不同阻尼因子归一化(相等ωn条件)后的冲激响应如图4所示。横坐标为ωnt，纵坐标为h(t)/(ωnA0)。

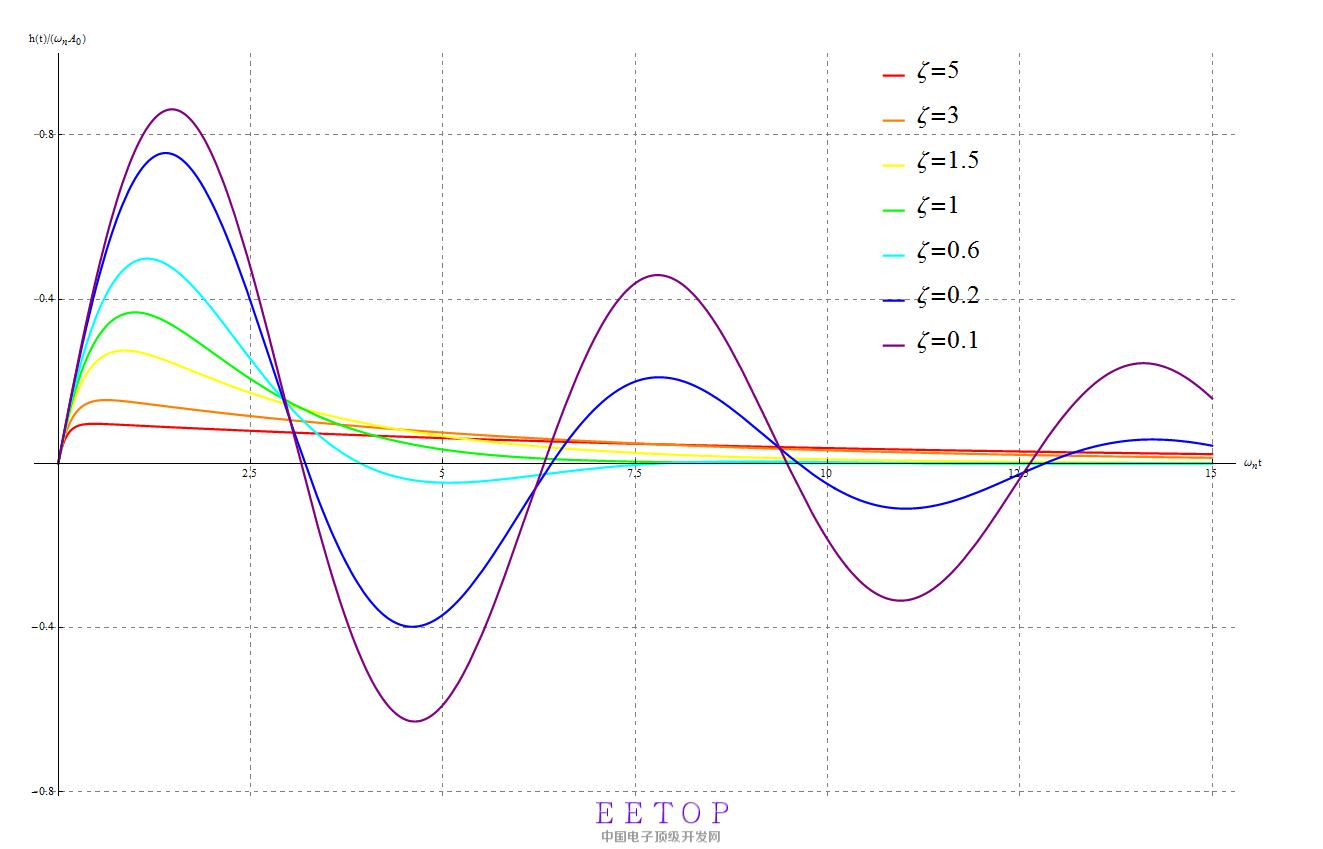
图4

阶跃响应

当输入信号为单位阶跃时，系统的输出为阶跃响应，通过求拉普拉斯变换及反变换，可以求得其时域的阶跃响应。同样也可以使用单位阶跃输入信号和冲激响应求卷积得到阶跃响应。

当阻尼因子0<ζ<1时，其阶跃响应瞬态分量包含了指数项和正弦项，指数衰减受阻尼因子影响，阻尼因子ζ越小，指数衰减速度越慢。正弦项的角频率也称为阻尼振荡频率，阻尼因子ζ越小，阻尼振荡频率越高，也越接近无阻尼振荡频率或自然频率。

图5

当阻尼因子ζ=1时，其阶跃响应瞬态分量包含了指数衰减项，线性项和指数衰减项乘积。其瞬态响应无超调量。

当阻尼因子ζ>1时，其时域表达式包含了两个指数衰减项，其中主极点ω1为慢速衰减项，主极点决定的瞬态分量，持续时间长，初始幅度大，在系统响应中起主导作用。次极点ω2为快速衰减项，其瞬态分量持续时间短，初始幅度小，在系统响应中起辅助作用。

不同阻尼因子时，其归一化后阶跃响应如图6所示。横坐标为ωnt，纵坐标为s(t)/A0。

图6

我们可以看到，在阻尼因子ζ<1时，阶跃响应存在超调量，但其瞬态响应有比较短的建立时间。过阻尼条件下，虽然无超调量，但建立过程比较慢。尽管有些系统中可能确实要求不能存在过冲情况。但大部分系统中为了追求比较快的建立，还是在系统设计中故意把阻尼因子ζ设计的稍微小于1。这也是二阶系统设计阶段需要折衷的地方。

这期我们先聊这么多，下一期，我们考虑模拟集成电路中由负反馈构成的二阶系统的一些结论。

阻尼震荡过程，PLL中常见的二阶响应

多谢分享

手动点赞

谢谢小编~

感谢分享

小编自己动手码的吧，辛苦了