温度而知新之二阶系统(下)

最近工作比较忙，更新比较慢，请大家多包涵。

温故而知新之二阶系统（上）http://bbs.eetop.cn/thread-625164-1-1.html

温故而知新之二阶系统（中）http://bbs.eetop.cn/thread-626580-1-1.html

错过的童鞋可以回顾一下前两期的内容。接上期分析，对于欠阻尼情况0<ζ<1，其瞬态响应存在的过冲归一化峰值时间及超调量如图1中公式所示，结果如图2所示。

图1

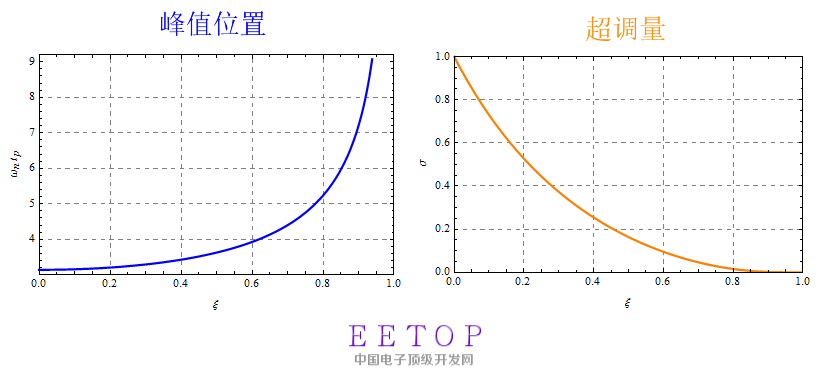
图2

在模拟电路中，经常使用的负反馈电路，需要考虑负反馈系统的稳定性。这里需要综合考虑放大器的主极点和次极点及反馈系数构成的负反馈系统是如何影响二阶系统的阻尼因子的。

图3

对于图3的所示的负反馈系统。前置放大器包含了主极点ω1st和次极点ω2nd,其传递函数表示为y(s)。假设反馈系数β，频率特性无相移。系统闭环响应A(s)如图4所示。低频增益表示为A0，频率响应表示为之前讨论的二阶系统的标准形式，可以得到无阻尼振荡频率和阻尼因子和前置放大器及反馈系数的关系。

图4

为得到图3系统的相位裕度，这里先得到环路增益(Loop Gain)的表达式，如图5所示。

图5

环路增益的幅频特性曲线穿越0dB（单位增益）的频率定义为穿越频率ωc（Cross Frequency），如图6所示。

图6

穿越频率和无阻尼振荡频率比值和阻尼系数的关系可以用图7表示。

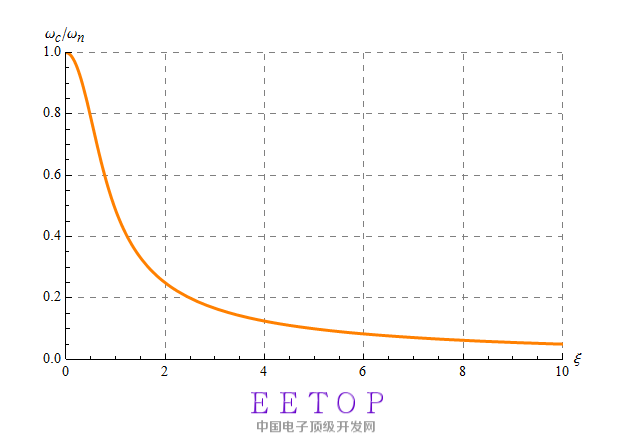
图7

相位频率表达式和相位裕度表达式如图8所示。

图8

相位裕度和阻尼因子的关系如图9所示。

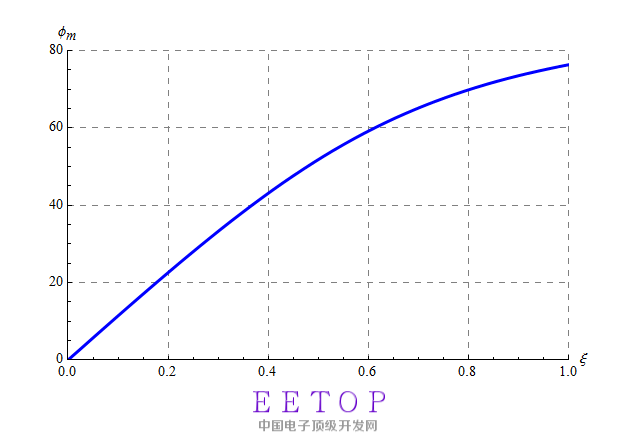
图9

我们看到，时域角度，超调量归一化峰值时间等，频域角度，穿越频率，相位裕度都和阻尼因子有关。这里把这些图汇总一下如图10所示。

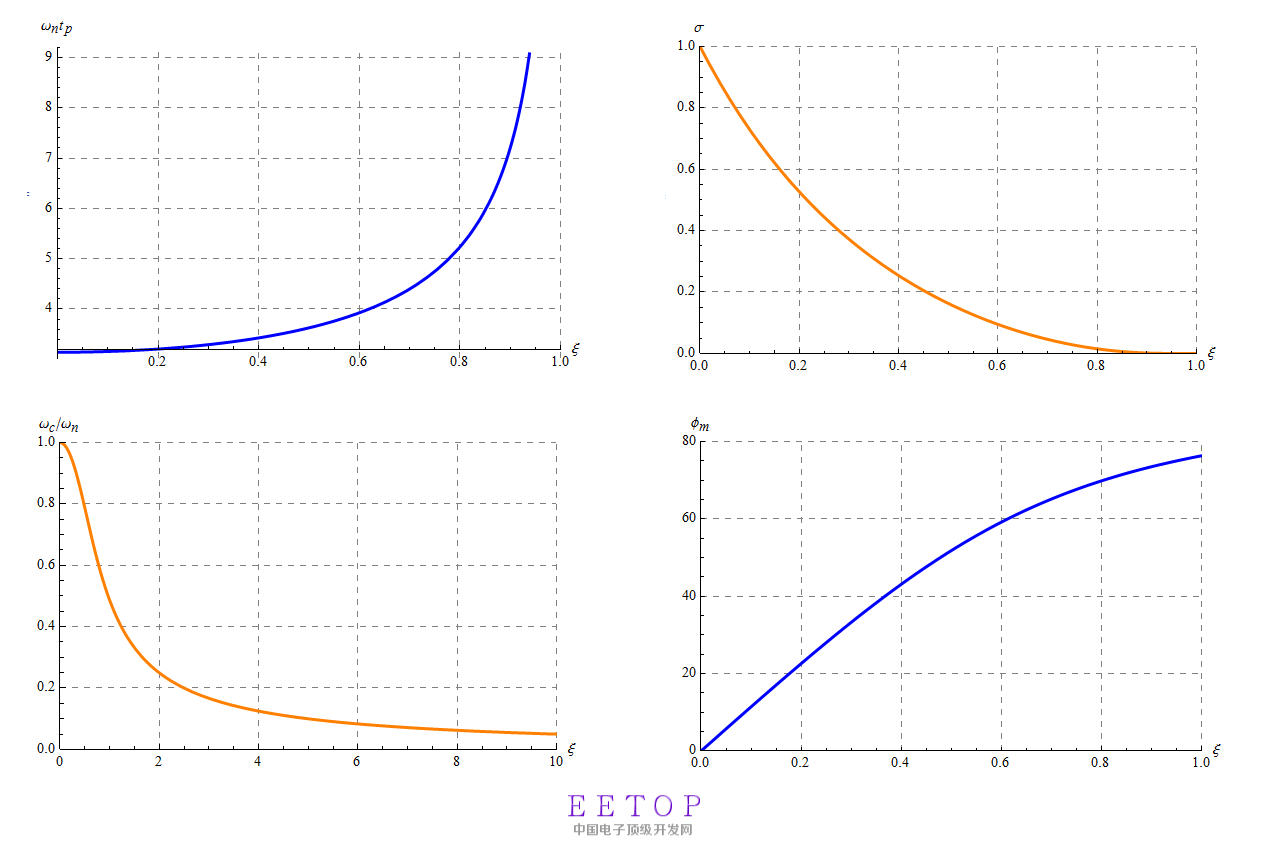
图10

通常，我们会通过时域的阶跃响应的过冲情况估算出阻尼因子，通过阻尼因子和相位裕度的关系，得到对应的相位裕度。这两者本质上是一致的。

通过3期的内容，相信大家会对二阶系统有比较系统，完善的回顾学习。其实，还有一点，就是运放次极点位置和GBW的相对位置，对PM的影响。这个我准备再补充一下，争取能更全面的把这部分内容融汇贯通。

好啦，这期就到这里了，下期见吧。

支持一下