认知无线电中的宽带频谱感知技术的FPGA实现

FT模块图

由上图我们可以看出，64点FFT我们可以调用16点FFT，16点FFT调用基四蝶形完成运算。基四蝶形运算单元的核心运算为加法和复数乘法，加法运算我们采用的是超前进位加法，运算速度较快。下面我们讨论高度优化复数乘法器设计

2.1高度优化复数乘法器设计

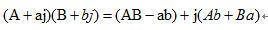
复乘的公式

下图为复数乘法器的并行实现框图：乘法器为自己设计的8位输入，16位输出。图中A+aj和B+bj为两个设计输入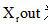，为输出的实部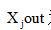，为输出的虚部。共需两级流水。

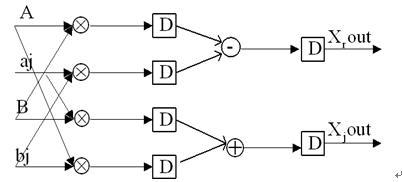
图四 复数乘法器

由于采用并行流水线FFT设计需要大量的slice，为了保证时钟频率达到要求的情况下最大可能的减少硬件开销，我们对复数乘法器中的旋转因子做了优化处理。

实际操作中，我们发现我们可以对复乘的公式做出相应的变形推导处理，可以看出其节约了乘法器的个数，而我们知道乘法器占用硬件面积较大，而当FFT点数较大的时候会节省较多的资源。而当FFT点数确定时， 旋转因子可以根据其周期性，对称性和欧拉公式做出相应变形，减少运算所需乘法器个数，节省了较大的硬件资源。

2.2基四蝶形单元设计

由基四FFT运算原理可得：x(n)为一长度为M的有限长序列定义x(n)的N点离散傅里叶变换为

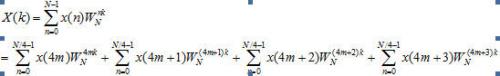
令：；；；；

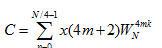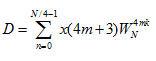则：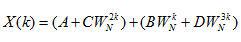

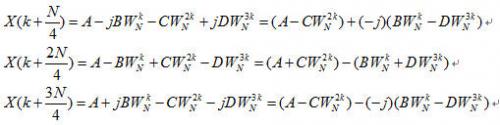
令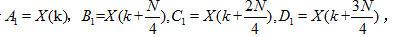，即

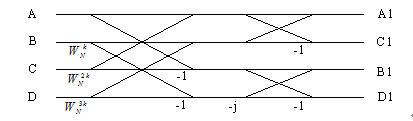
图五 基四FFT基本信号流图

2.3 16点FFT的流水线实现

16点FFT是64点FFT的重要部分，以下为16点FFT的流水线实现图。为了保证在满足系统时钟频率要求的情况下，最大可能的减少硬件开销，我们利用旋转因子的周期性和对称性对16点FFT进行了乘法器和旋转因子的优化，节约了较多的slice。

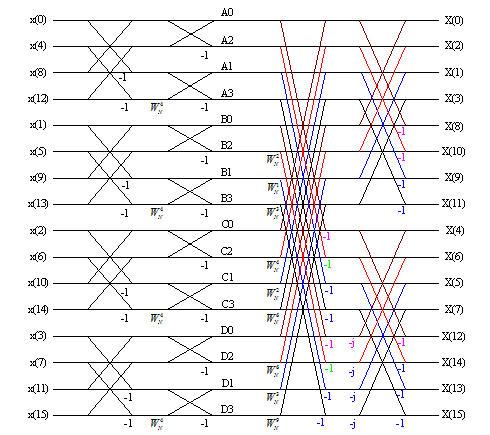
图六16点FFT的流水线实现图

（三）克服噪声不确定度算法模块

能量检测能实现盲感知且实现简单而被广泛采用。然而能量检测的性能依赖于估计的噪声功率值，这样即使一个非常小的噪声功率估计偏差都会造成能量检测性能的急剧下降。因此能量我们不仅要进行能量检测，而且要克服噪声不确定度的影响。

能量检测具有两个重要性能指标：

虚警概率P_f ，假设环境中仅有噪声，检测系统确检测到信号存在的概率。

检测概率P_d，假设环境中存在信号，检测系统检测到信号存在的概率。

在认知无线电系统中，高的虚警概率会导致低的频谱利用率。在加性高斯白噪声信道（简称AWGN信道）下，虚警概率和检测概率的表达式如下：

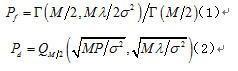
在这里假定噪声为加性高斯白噪声，功率为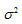，采样点数为M，信号功率为P。

观察上述两个性能指标的公式，我们也可以看到虚警和检测概率功率与噪声功率的大小密切相关。因此噪声不确定度（噪声功率随时间而变化）严重影响能量检测的性能。

图七 能量检测性能曲线

在信号噪声功率比为5dB,采样点数为M为200时，我们观察能量检测性能曲线发现，随着噪声不确定度的漏警概率（P_m=1- P_d )迅速增大，特别是噪声不确定为2dB时的能量检测性能与理想能量检测（噪声不确定度为0dB）相差极大, 如虚警概率为0.1时， 理想能量检测的漏检概率为0.06，而噪声不确定度为2dB时的漏检概率为0.6，性能降低了一个数量级。因此克服噪声不确定度是能量检测可以广泛应用的关键技术

常见的噪声不确定度的算法有FCME算法、多天线技术和特征值技术等，但是后两者实现起来非常困难。而FCME算法不仅实现起来比较简单，而且性能较好。

FCME算法可以有效的克服噪声不确定度。它的中心思想就是利用多信道中已经存在的空闲信道，提取噪声信息，确定噪声的功率，自适应提取门限，确定被占用信道，大大提高了检测性能。

FCME算法有很多优点：

1）采用能量检测，实现简单。

2）能有效克服噪声不确定度的影响，提高检测的可靠性。

3）采用快速高效的排序，提高检测效率。

4）信道化检测，实现宽带感知。

FCME算法原理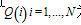：为信道的能量，并以升序排列，其中N是信道数目。假设前I个能量最小的信道仅包含噪声。FCME算法就从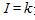开始执行检测公式

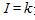
如果公式成立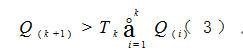，所在信道均包含信号，算法停止运算。否则，K增加1继续检测直到算法成立。其中Tk 是与虚警概率相关的比例因子。

基于算法原理，我们在这里做了模拟仿真，设定信道数N为32，I为8，采样点数M为5。仿真结果如下图八：

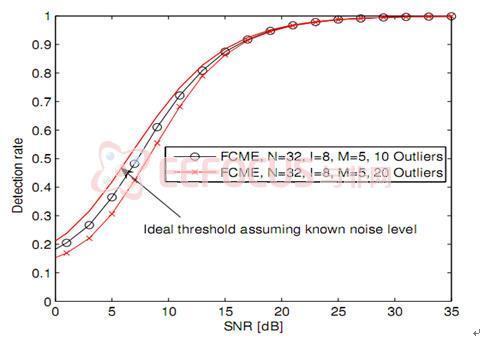
图八 FCME性能曲线

可以观察到，FCME算法的性能与理想能量检测的性能十分接近，有效的克服了噪声不确定的影响。其算法实现框图如下：

图九FCME算法实现框图

求得每个信道的能量，然后对能量进行升序排列，设定I值，执行FCME比较。可以看出，高速低延时的排序算法是FCME算法的核心部分。

排序算法是FCME算法