模糊传感器的研究意义、概念、理论基础
模糊传感器是在20世纪80年代末出现的术语。随着模糊理论技术的发展,模糊传感器也得到了国内外学者们的广泛关注。模糊传感器是在经典传感器数值测量的基础上,经过模糊推理与知识集成,以自然语言符号描述的形式输出测量结果的智能传感器。一般认为,模糊传感器是以数值量为基础,能产生和处理与其相关测量的符号信息的传感器件。
二、模糊传感器的研究意义
传统的传感器是数值传感器,它将被测量映射到实数集中,以数值符号来描述被测量状态,即对被测对象给以定量的描述。这种方法既精确又严谨,还可以给出许多定量的算术表达式,但随着测量领域的不断扩大与深化,由于被测对象的多维性,被分析问题的复杂性或信息的直接获取、存储方面的困难等等原因,只进行单纯的数值测量且对测量结果以数值符号来描述,这样做有很大缺陷,例如:
(1)某些信息难以用数值符号来描述。例如在产品质量评定中,人们常用的是"优"、"次优"、"合格"、"不合格",也可用数字1,2,3,4来描述,但数字在这里已失去通常的测量值的意义,它仅作为一个符号,不能来表征被测实体的具体特征。
(2)很多数值化的测量结果不易理解。如在测量人体血压时,人们更关注的是:老年人的血压是否正常,青年人的血压是否偏高。而实测的数据往往不能被普通人读懂,因而满足不了人们的需求。
因此,有待用新的测量理论和方法来补充。模糊传感器正是顺应人类的生活实践、生产与科学实践的需要而提出的。
三、模糊传感器的理论基础
1、符号化表示原理
模糊语言是人类表述语言的一种,因为人们对自然界事物的认识存在着一定的模糊性,用模糊符号来表述信息具有较为简单、方便,且易于进行高层逻辑推理等优点。模糊符号化表示就是利用模糊数学的理论和方法,借助于专门的技术工具,把测量得到的信息,用适合人们模糊概念的模糊语言符号加以描述的过程。符号是信息的载体,是对一个物体或事件状态的描述,它定义了实体的特征属性或实体间的关系。设Q为数值域,S为语言域,在各自的论域上有若干个元素qi、si,且表示为:
Q=〈q1,q2,…〉 qi∈Q (1)
S=〈s1,s2,…〉 si∈S (2)
同时,在论域Q和S上分别定义一组关系族:
R=〈R1,R2, …,Rn〉 Ri Q×Q×…×Q (3)
P=〈P1×P2×…×Pn〉 Pi S×S×…×S (4)
并且定义:D=〈Q,R〉,L=〈S,P〉
其中,D-对象关系系统,描述数值域元素及其相互关系;
L-符号关系系统,描述符号域元素及其相互关系。
设有两个映射M和F,M:Q→S,使得Si=M(qi),F:R→P,使得Pi=F(Ri)成立,且M Q×S和(qi,si) M,则称si是qi的一个符号。si的含义是qi从数值域下向语言域映射的投影,而对每一次测量qi,符号si成为qi的描述。系统原理如图1所示。
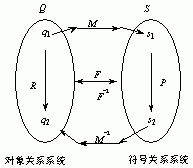
图1 符号化表示原理示意图
如果F映射是一对一映射,而M映射是同态映射,那么一定存在逆映射:F-1(Pi)=Ri,M-1(si)=qi。M映射可以是"单对单"或"多对单"映射。那么,在后一种情况下,符号域中的一个符号经M-1映射在数值域对应出的不是一个点,而是一个"子域"。因此,模糊符号化表示有一定的局限性,即在不同测量结构下,同一测量子集的元素对应不同的符号;或在同一测量结构下,存在测量子集的一些元素同时对应于不同的符号的情况。这一局限性可通过基于多值逻辑理论的多值符号化测量来弥补。其基本思想是:在实体测量集中,根据对实体的某一特征表现程度的不同,把测量子集Q中的元素按特征隶属度最大归类于某一子集,忽略其他特征的表现,因此只要在测量集上对实体集选取适当多个特征表示,使之与测量集中的元素相对应,就可把Q分成有限个意义相关又表现不同的子集{Qi},对每一个Qi进行符号映射,从而实现对实体集多值符号化测量。
2、多级映射原理
虽然符号具有高级逻辑表达、易理解、人类经验与知识易集成、较宽的冗余度等特点,但与数值测量无限可分相比,符号化测量描述细节的程度和范围不够,尤其在利用符号对数值转换实现定量测量时更为突出。而多级映射原理在实现数值对符号和符号对数值转换的同时,可以扩大符号表示的细致程度和范围。
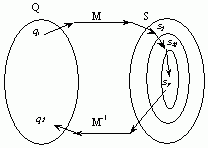
图2 多级映射原理示意图
本文概述了模糊传感器的研究意义及概念,简要介绍了模糊传感器的理论基础及实现方法,并举例说明了模糊传感器的应用。
多级映射的基本功能是实现数值→符号的变换和符号→数值变换。其原理如图2所示,它的信息传输分为两种情况:
首先是数值对符号的转换,并且是由数值域Q中的元素qi经过映射M的第一级M1映射到符号域S的子集Si,如果子集Si描述细致程度不够,则可以进行第二级映射M2,映射M2将qi映射到次子集Sij,经过若干级映射可以得到描述qi信息的符号sy;
其次,则是符号对数值的转换,由经过多级映射得到的符号sy通过映射M-1得到数字值qj。
由于自然语言表现概念的局限性,建议多级映射的级数为3级。例如,对于0℃~100℃的温度范围,每级采用7个概念,在映射级数为3级时,精度达到0.3℃。对于不需要人们直接参与的中间测量结果情况,多级映射级数可以根据需要加以确定。映射级数的多少另一方面还取决于每一级中包含概念(元素)的个数,每一级概念个数多则需要的映射级数就相应少。如果多级映射应用于包含数值输出在内的模糊传感器研究,则映射级数和传感器变换非线性误差是相关的,映射级数应该通过给定的测量不确定度加以确定。
