无线Ad hoc网络一种最小化链路干扰的载波监听机制设计

无线Ad hoc网络中，干扰产生于接收节点处的接收信号被其他无用信号叠加，干扰问题严重影响接收端解码信息的能力，导致数据包冲突和重传的增加。如何最小化链路干扰，减少数据包冲突概率，是提高网络性能的关键。MAC协议中，合理的载波监听机制是减小链路干扰的有效方式之一，通过合适的感知门限设计，可以有效地降低链路中的干扰和冲突，提高网络吞吐量。文章提出一种最小化链路干扰的载波监听机制，该机制根据链路的实际状况对接收节点的干扰范围进行计算，进而使得发送节点调节合适的感知门限值，使发送节点可以感知到所有干扰节点，进而最小化链路干扰。模拟结果显示，本文提出的机制能有效地提高网络吞吐量，最小化数据包冲突概率和链路中存在的干扰。

0 引言
无线Ad hoc网络是由一组可以自由移动的节点构成的多跳无线网络，又称自组织网和多跳网。干扰产生于同一空间内的多个同时传输节点相互之间的信号作用。因为无线自组织网中的数据是通过无线电形式传播，如果一个正在传输的链路周围存在其他无用的无线电信号，则在此链路上造成了干扰，较轻的干扰会造成误码率提高，部分数据包丢失；较重的干扰会造成传输失败，链路断开。产生干扰的节点处于接收节点的周围，其存在的根本原因是发送节点在发送数据之前无法有效感知到这些干扰节点。无线Ad hoc网络中每个节点的发送功率无法无限增大，每个节点的通信距离也根据自身功率的大小不尽相同，所以，每一个节点都存在着通讯半径和干扰半径。这两个半径中，通讯半径保证了节点在此范围内能够接收到信号，如果干扰值被控制在一定范围之内，则可以正确接收信号；干扰半径(din)表示节点受到干扰的区域，这一干扰区域的大小也和周围节点的发送功率有关。
设计合理的载波监听机制是降低干扰的有效途径之一。其中，基于IEEE 802．11协议的载波监听机制得到了最广泛的应用。载波监听机制规定：节点在发送数据之前，首先检测周围信道的信号强度，如果检测到的信号强度大于感知门限值(CSth)，则表明此时信道处于繁忙状态，节点进入退避过程；如果检测到的信号强度小于感知门限值，则进行数据发送。所以，通过合理设置载波监听机制中的感知门限值，可以使得发送节点在传输数据之前感知到周围节点对接收节点的干扰，从而判断是否进行数据的发送。载波监听机制中，每个节点的感知门限值(CSth)对应一个感知范围(Carrier Sense Area)。如果网络中的节点采用相同的传输功率，则感知范围可以形式化为一个圆，此圆的半径即被称为感知半径(din)，感知半径和感知门限值成反比。
与载波监听机制相比，RTS-CTS机制通过RTS-CTS-DATA-ACK四次握手和网络分配向量(NAV)的设置实现信道的预置和占用。但是，RTS-CTS机制因为控制包的发送范围有限，接收节点无法将CTS包发送至周围所有的干扰节点；同时，RTS／CTS控制包发送范围固定，无法根据干扰范围和链路的实际情况进行发送距离调节。所以，RTS-CTS机制对接收节点周围存在的干扰控制能力有限。然而，通过载波监听机制的设计，可以根据链路状况选择合适的感知门限，确定合适的感知半径，使得发送节点感知到所有干扰节点，从而最小化链路中存在的干扰。
本文提出最小化链路干扰的载波监听机制。接收节点首先根据链路状态对其干扰范围进行计算；再将计算值反馈给发送节点，使得发送节点精确调节自身感知门限使其可以感知到链路周围所有的干扰节点，从而最小化链路干扰。

1 干扰模型
本节内容对接收节点的干扰范围进行形式化描述并计算干扰半径，进而考虑干扰信号的累加问题，进一步得到修正后的干扰半径。本节所提出的干扰模型，与传统干扰模型相比更为精确。
1. 1 干扰半径计算

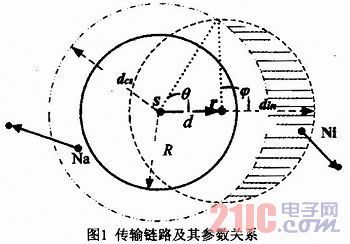
如图1所示，接收节点r接收到的信号强度Pr随着发送节点s和接收节点r之间的距离d的增大而减小，随着距离d的减小而增大。Ps定义为发送节点s的发送功率，g是天线增益，a是路径衰减指数(Path Loss Exponent)，这一指数通常选择2到4之间的整数。所以，在接收节点r处收到发送节点s的信号强度为：


当发送节点s向接收节点r发送数据时，位于发送节点s的感知范围之外的另一个节点Ni也试图发送数据，节点s没有感知到节点Ni的存在，便产生了干扰。这样，s和Ni两个节点发送的信号在接收节点r处产生叠加。s的信号能否顺利被r所接收，取决于捕获效应(Capture Effect)。对于捕获效应来说，如果在接收节点处s产生的信号比Ni产生的信号足够强，那么r将会顺利接收到s发来的数据，Ni产生的虚弱信号会被当作噪声加以忽略。本文采用信噪比(SIR)模型描述捕获效应：如果接收节点收到的信号强度与干扰信号之比大于一定的门限值β时，接收节点可以成功接收信号：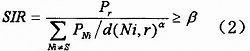


根据信噪比模型，本文定义接收节点r的干扰区域节点的集合INr(INr也可以表示接收节点r的干扰区域)为：


因此，干扰区域的半径din为干扰区域中din(Ni,r)的最大值，根据式(3)，同时，我们设定网络中所有节点的发送功率相同，有PNi=Ps，得到：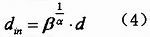


从式(4)可以看出，接收节点的干扰半径主要与信噪比门限值和发送节点与接收节点之间的距离有关。
1．2 干扰半径修正值
本文注意到，在接收节点r的干扰范围外，其他节点的同时发送会在r处叠加信号功率，形成虚拟的干扰节点。因而有效的干扰区域要大于式(4)计算的干扰范围。所以，需要对式(4)干扰半径进行修正。
设网络密度为δ，在半径为din的干扰范围内，干扰节点数可以表示为：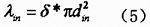


在式(4)的干扰范围之外，存在虚拟的干扰节点。考虑一个以节点r为中心的微小圆环Ri，内部半径为ri=din+(i-1)△r，外部半径为ri+△r，该圆环内部所有的节点在r处产生的信号功率都简化地视为一样，进而可以用积分求得外部信号叠加形成的虚拟干扰个数：