并行ADC性能扩展一种比特滑动流水模

摘要：根据现代通信对模数转换的高速、高分辨率性能要求，在对现有的并行式模数转换电路研究和改进的基础上，提出了一种比特滑动流水并行式模数转换方法，从而简化了电路结构、节省了器件、降低了功耗，更有利于集成化。时域仿真实验结果表明，运用该方法实现的ADC，其采样频率达到 10Ms/s。
关键词：分段量化；流水；并行；模数转换

中图分类号：TN702 文献标识码：A 文章编号：1003-353X(2003)06-0029-04 

1 引言

随着现代通信领域中技术发展的突飞猛进，整机系统对模数转换提出了更高的要求。例如软件无线电系统，其中的关键问题就是模数转换电路的高速（即高转换速率或高采样频率）、高分辨率（即高转换位数）等性能要求的实现 [1]。在高速领域，现有的模数转换以并行转换为主，但是由于其电路规模随着分辨率的提高而呈指数式的增长（即2N -1，N为转换位数）以及由2N-1 个比较器的亚稳态 和失配而引起的闪烁码所造成的输出不稳定，很难实现8位以上的高分辨率，而且功耗和体积较大，难以满足实际使用的要求 [2]。针对并行模数转换的局限，本文提出了一种采用分段量化和比特滑动技术的流水并行式模数转换电路，较好地结合了并行式和逐次逼近比较式两种模数转换各自的长处，在保证高速工作的同时，可实现并行式难以实现的8位以上的高分辨率模数转换，而且比现有的流水并行式模数转换电路[3,4]更进一步简化结构、减少寄存器数量、降低功耗，更有利于集成化。

2分段量化的逐次逼近比较模数转换

假设对任意波形信号在某一时刻采样值 A0进行n位的二进制量化结果为： D1D2…Dn ，则A0可以表示为：

A0=VR(D1+D-2+…+2-(n-1)Dn)+δn(1)
其中，是A0经过 n位二进制量化后的量化误差，D1 是A0与VR相比较的结果：

D1=1 A0VR0A0VR

将其适当变形后可得：

A0=VRD1+VR(2-1+…+2-(n-1)Dn)+δn(2)

将（2）式中的2-1D 2移至等式的左边，然后等式两边同时乘以2得：重复上述过程可得：

A1=2(A0-VRD1)=VRD2+VR(2-1D3+…+2-(n-2)Dn)+22+δn(3)

重复上述过程可得：

A1=2(A0-VRD1)=VRD2+VR(2-1D4+…+2-(n-3)Dn)+22δn

 An=2(An-1-VRDN)=2nδn(4)

其中，Di+1 是Ai与VR相比较的结果：

Di+1=1AVR0AVR i=0,1,n-1(5)

 Ai+1=2(Ai-VRDi+1)(6)

现再假设对A0进行 k位的二进制量化(2≤k<n)，其结果为： d1d2…dn ，则A0可以表示为：

A0=VR(d1+2-1d2+…+2-(n-1)dk)+δk（7）

其中，δk是A0经过 k位二进制量化后的量化误差，重复上述过程可得：

A1=2(A0-VRD1)=VRD2+VR(2-1D4+…+2-(n-2)dk)+2δk

 Ak=2(Ak-1-VRDN)=2kδk(8)

其中，di+1是与 VR相比较的结果（i=0,1,…, k-1。）。然后再设对Ak进行n -k位的二进制量化的结果为：dk+ 1dk+2…d n，则Ak又可以表示为：

Ak=VR(d=+1+2-1dk+2+…+2-(n-2)dn)+δn 

其中，是经过n-k位二进制量化后的量化误差，重复上述过程可得：

Ak+1=2(Ak--VRdk+1)

 =VRD2+VR(2-1D4+…+2-(n-2)dk)+2δn

 An=2(An-1-VRdn)=2(n-k) δn

其中，di+1 是与VR相比较的结果（i=k ,k+1…,n-1。）。

由（2）、（7）两式可得，D 1和d1都是A0 与VR相比较的结果，因此有：d 1=D1。再由（3）、（8）两式可得：。如此一直递推下去，最后可得：d2= D2，，…，dn=D n，，。这样就证明了对任意波形信号电压A 0进行一次n位二进制量化和i次分段 ni位二进制量化（∑ni=n）是等效的，而且，其模拟余量A n也可以用于扩展模数转换的量化比特数（即提高转换的分辨率）。 因此，完全可以将模拟信号先经过位数较少的模数转换电路进行粗转换，然后将其模拟余量再送入多位高速并行模数转换电路进行高速、高分辨率的模数转换。

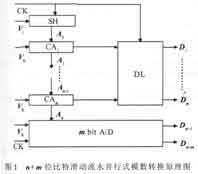
3 比特滑动流水并行式模数转换

现有流水并行式模数转换就是将延迟逐次比较式A/D转换电路[4]在时间上的串行工作转化为单个模块的流水式串行工作，对输入信号进行粗转换，然后再采用多位高速并行模数转换电路对粗转换的模拟余量进行高速、高分辨率的模数转换。

在12位流水并行式模数转换电路[5] 中，转换时间为：

t31c=t1c=t3ctCA+tSH(9)
 
而与位数 n无关。其中，t31C是整个模数转换电路的转换时间，t1C是8位并行模数转换电路的转换时间，t3C是流水式电路的转换时间， tCA是流水式电路的比较单元CA的延迟时间， tSH是流水式电路的采样保持单元SH的采样保持时间。这种模数转换电路由于受到tCA和tSH 的限制，转换速率难以进一步提高。