中国“量子通信”书写传奇 筹划发射新型通信卫星

被认为与量子纠缠密切相关的宇宙虫洞想象图

潘建伟(中)和他的研究团队
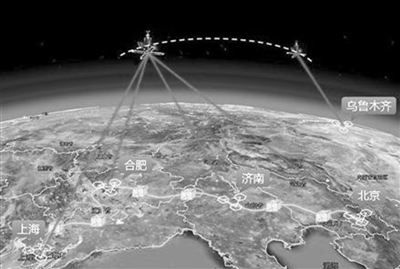
星地间量子通信示意图

在2015年国家科学技术奖励大会上,一支由中国科技大学的"70后"院士、"80后"教授组成的"青春战队"格外引人注目。他们在中科院院士潘建伟带领下,凭借"多光子纠缠和干涉度量学",奋力摘得国家自然科学一等奖。他们所研究的光子,是量子的一种。
量子是一个能量的最小单位,所有微观粒子如分子、原子、电子、光子等都是量子的一种表现形态。我们看到的光,就是由数以万亿计的光量子组成的。研究量子有什么用?用处很多,比如:利用量子纠缠,我们的通信将能实现绝对安全,让"棱镜门"等泄密事件从此作古;若制造出100 个粒子纠缠的量子计算机,其计算速度将比目前最快的超级计算机"天河二号"还快百亿亿倍。更神奇的是,利用量子隐形传态,未来人类往返世界各地,甚至进行星际旅行,需要的时间也仅仅是"嗖"的一下。
事实上,中国的量子通信技术已达到世界顶尖水平,领先欧美国家。今年,世界上第一条量子通信保密干线"京沪干线"将开通。同时,由中国科学家自主研发的世界首颗"量子科学实验卫星"也发射在即。潘建伟在接受采访时表示,我国正以这两大工程构建一个天地一体化的量子通信网络雏形,最终目标是建立一个覆盖全国甚至覆盖全球的广域量子保密通讯网络。
猫如何既是死的又是活的?
要说清楚量子通信的宏伟蓝图,我们还得从量子力学讲起。这是一个与牛顿力学等经典力学差异很大的物理学分支,被誉为迄今为止描述微观世界最准确的理论。
量子是什么?通俗地解释就是把能量等物理量一份份往下分,分到无法再分的小块儿,这个小块就是量子。如氢原子中电子的能量只能取一个基本值——-13.6电子伏特或者其1/4、1/9、1/16、1/25 等,而不能取其2 倍或1/2、1/3。这就好比上台阶,只能上一个台阶,而不能上半个。
量子力学和经典力学的根本区别在于确定性问题。与我们常识里的事物具有确定的位置相反,量子力学中的粒子状态是不确定的,而且是一种客观真实的状态。这种状态有两个基本原理。
一个是量子态叠加原理。根据量子力学理论,物质在微观尺度上存在两种完全相反状态并存的奇特状况。如何来证明这种原理呢?奥地利物理学家薛定谔在1935年提出的"薛定谔猫"佯谬提供了一种思路。
"薛定谔猫"佯谬假设了这样一种情况:将一只猫关在装有少量镭和氰化物的密闭容器里。镭的衰变存在几率,如果镭发生衰变,会触发机关打碎装有氰化物的瓶子,猫就会死;如果镭不发生衰变,猫就存活。根据量子力学理论,由于放射性的镭处于衰变和没有衰变两种状态的叠加,猫就理应处于死猫和活猫的叠加状态。
这只既死又活的猫就是量子物理界著名的"薛定谔猫"。如果把量子叠加原理合到多个量子的情况会是什么呢?这就是量子力学的另一个基本原理——爱因斯坦称为"遥远距离诡异的相互作用"的量子纠缠。就像双胞胎心灵感应一样,这两颗骰子无论相距多远,掷出来的结果始终是一样的(当然,爱因斯坦坚称"上帝不会掷骰子")。
我们再以"薛定谔猫"来解释:整个状态现在处于镭是否发生衰变和猫是死是活的叠加状态,用一个等式来表示就是:整体状态=镭发生衰变而且猫死了(A)+镭没有发生衰变而且猫活着(B)。当你打开容器盖子观看猫是不是死了的那一刻,整个状态就被确定了,要么是A,要么是B,而且另一种状态也跟着消失了。这就是量子的纠缠态。在量子世界中,处于纠缠态的两个粒子不论分开多远,如果对其中一个粒子作用,另一个粒子就会立即发生相应变化,而且不受时空限制,是瞬时变化。
绝对不会被破译的通信
如此神秘的量子叠加原理和量子纠缠,我们到底能拿它来做些什么呢?一个已经被潘建伟团队研究得很成熟的应用是量子保密通讯。
现在被认为最安全的信息传递方式是光纤通讯。光缆能把所有的光能限制在光纤里,外面得不到能量,所以这个传输被认为是安全的。但随着科技发展,只需让光缆泄露哪怕很少一部分能量,我们就能够窃听光缆传递的信号。潘建伟解释说,这是因为经典通信的信号只有0和1,发生窃听时,这两种信号不会被扰动。如两人打电话时,他人可通过窃听器,从通信线路中的上千万个电子中分出一些电子,使其进入另一根线路,从而实现窃听,而通话者无法察觉。
量子通信则完全不会出现这个问题。除了因为量子信号有0、1、0+1、0-1等量子叠加态,还因为量子由这种叠加态而产生的不可克隆原理。根据量子力学理论,对任意一个未知的量子态进行完全相同的复制的过程是不可实现的。也就
量子通信 相关文章:
- 我国大尺度量子信息处理实验成果获国际学术界高度评价(01-27)
- 德科学家实现物质量子比特遥传距离21米新高(04-22)
- 中科院成功完成星地量子通信地基验证试验(05-02)
- 真正保密的通信:量子通信(06-17)
- 2013年5月《自然》杂志内容精选(07-10)
- 中科院光电所研制望远镜为量子通信打基础(07-28)
