有源滤波器与全极点滤波器介绍

 有源滤波器按传输函数的极、零点分类

全极点型滤波器

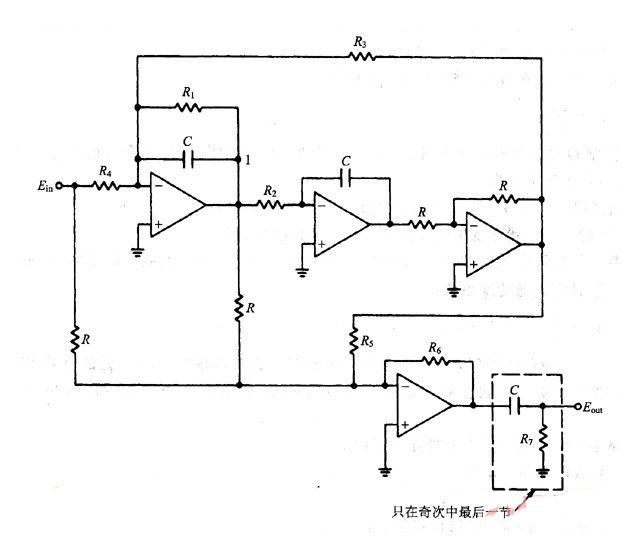
以上介绍的巴特沃斯、切比雪夫、贝塞尔等三种滤波器，它们的共同特点是传递函数的零点在无限频处。也就是说，这些滤波器只有在无限频处才能给出无穷大的衰减，称之为全极点滤波器。

非全极点滤波器

如椭圆函数滤波器和反切比雪夫滤波器的共同特点是传递函中既含零点也含极点、这样就能在限频处获得无穷大的衰减。以上两种滤波器均是非全极点滤波器。上述滤波器均是非全极点滤波器。

上述滤波器，它们各有特点，在实际应用中，应该根据实际要求来选择滤波器的类型。

如果要求通带响应平坦，对截频衰减陡度要求不太高，阶跃响应允许有过冲的话，则应采用巴特沃斯滤波器。若对幅度平坦性要求不严，而对截止频衰减陡度要求较高的情况，应采用切比雪夫滤波器。而对那此在不失真地再现信号这一要求比衰减特性更重要的场合下，则应采用贝塞尔滤波器。由于椭圆滤波器比其他类型滤波器，才使用椭圆滤波器。对于中等程度要求的滤波器来说，全极点滤波器是完全能满足要求的。