灰色预测控制在有源滤波器中的设计应用
为了保证有源电力滤波器的工作性能,实时准确的检测出负载中的谐波分量,获取正确的谐波补偿信号至关重要。目前谐波电流检测的主要方法有基于瞬时无功功率理论、基于频域分析的快速傅里叶变换(FFT)和自适应[3,4]等方法,但这些方法涉及参数多,计算量大,过程复杂,尤其是对APF 系统延迟问题。针对数字化的APF系统内部结构固有的延迟特点,运用灰色系统理论的GM(1,1)灰色预测模型,提出基于灰色预测的APF 预测控制方案。
无源滤波器利用电容和电感谐振的特点来抑制特定频率的高次谐波分量和提高功率因数,体积大、滤波频率固定和会出现串/并联谐振等缺点,限制了它的广泛使用[1];近十年来,有源电力滤波器(Active Power Filters)以其可补偿各次谐波,还可以抑制闪变、补偿无功,有一机多能的特点,引起人们的广泛重视,这一新型的谐波抑制装置有着广阔的发展应用前景。与无源滤波器相比,有源电力滤波器能够实现动态补偿,并具有体积小,不易发生谐振等优点[2]。
2.系统的实现
2.1APF 系统的工作原理和数学模型
并联型有源滤波器电路原理图如图1 所示,其中us 和uc 分别为电网电源相电压和逆变器输出相电压,L 为扼流电感,R 为电感内阻及线路的等效电阻。设系统的三相平衡,系统可用单相来近似描述。电流Li和APF输出的补偿电流ci由图1可得APF 的数学模型。
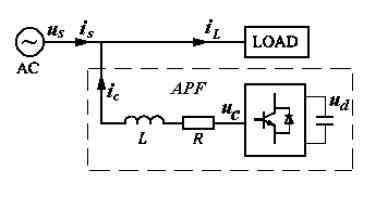
图1 APF 主电路框图
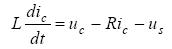
在APF中,快速实时跟踪负荷中谐波电流的变化时,通常是当前时刻检测出负载的谐波电流和补偿电流,计算出下一时刻逆变器的补偿量,即给系统带来至少一个采样周期的延迟。此外,系统受电压、电流的采样、输入滤波器的相位滞后和参数计算所需的运算时间等的影响同样会给系统的控制带来时间的滞后。控制的时延将会直接影响系统的性能和稳定性。
设系统信号输入滤波器为一理想环节,对补偿范围内的谐波分量不带来相位滞后,通过选用高A/D 转换器和数据处理器使系统的数据处理和控制信号的产生在功率开关器件一个开关周期内完成。即构成的离散控制系统,从信号的采样到形成PWM 电压指令,并在下一个开关周期产生脉宽调制信号由逆变器输出,即最少延迟了约一个开关周期。系统电流环的结构图可写为
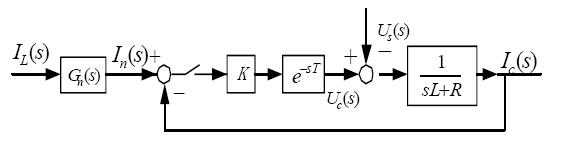
图2 系统结构框图
其中Gn (s) 、K 、e−sT 分别为谐波检测环节、逆变器、电流比例调节器、延迟环节的传递函数。其中PWM 逆变器的输出电压uc 在一个采样周期得平均值就是uc 。
2.2APF 的灰色预测控制系统的实现
图3为APF灰色预测控制系统的结构框图,系统通过采样装置在k时刻对负载电流和APF输出补偿电流进行采集和整理;由灰色预测装置建模,得出k+1时刻负载谐波电流;由APF的模型、控制量和ic (k) ,预测出APF输出的电流在k+1时刻的值iˆc (k + 1) ;确定控制量,使未来的输出ic 尽量接近目标。

图3 灰色预测控制系统的结构图
2.2.1负载的谐波电流的预测
为了不断把新得到的数据考虑进去, 这就要求将每一个新得到的数据送入原始序列X (0) 中,重建GM(1,1), 重新预测, 我们把它称为新息模型。采用这种新息模型,随着时间的推移, 新息越来越多, 存贮量不断扩大,运算量也不断增加, 这既不适合工业过程控制对实时性、快速性的要求, 而且老数据的信息意义会随时间的推移而降低, 甚至会淹没新信息。为了克服这一矛盾,在这里每补充一个新信息的同时去掉一个老信息,以便在滚动建模时维持原始序列数据个数n不变。
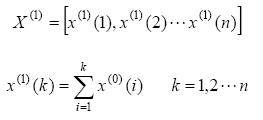
可得系统的谐波电流(k+1)时刻的预测值
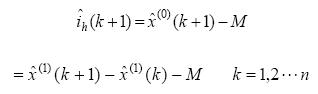
2.2.2 APF补偿电流的预测
对应的离散方程可近似描述为:
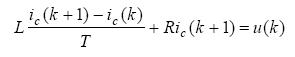
其中T为系统采样周期,则可得APF补偿电流的k+1时刻预测值
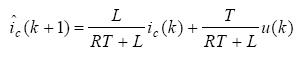
取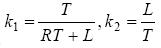 ,则上式可改写为
,则上式可改写为
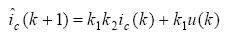
2.2.3 控制律的设计
取目标函数
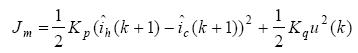
令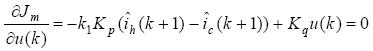
则可得系统得优化控制律
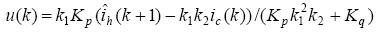
3.系统的仿真
取系统的非线性负载采用三相不可控整流电路,系统的非线性负载电流和谐波电流波形如图6所示。取系统的采样频率fs =10kHz ,L=1mH,R=0.5Ω,Kp =Kq =1,运算过程中的序列组元素个数n=5,采用GM(1,1)对系统谐波信号进行预测,系统的仿真结果如图4所示:
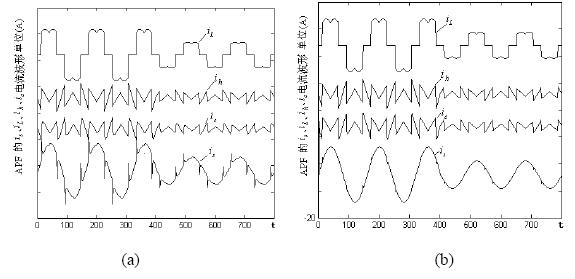
图4 电网经APF补偿后的负载电流波形
采用图2和图3系统控制后系统各部分电流波形分别如图4(a)、(b)所示。对比图4(a)和(b)可见,采用灰色预测控制能较好克服APF滞后对谐波补偿的影响,改善了系统的性能。
本研究取得以下创新点:
(1)提出了基于灰色预测的APF预测控制方案;
(2)应用灰色系统理论建立了负荷谐波电流的GM(1,1)预测模型,在第k 步预报出第k+1 步的谐波电流iˆh (k + 1) ,在此基础上来实现补偿分量对负载
- 一种新颖的密封铅酸电池充电器的设计与应用(01-09)
