微驱动器的电磁与运动分析及仿真

 0引言

微驱动器作为微机电系统(MEMS)的驱动部件，已得到广泛研究。近年来，采用硬磁和软磁材料构成的驱动器在微机电系统和微光机电系统中受到了越来越多的关注，这主要由于电磁驱动方式能够在较大的范围内提供足够的驱动力，并且能够进行远程驱动控制，响应速度快。尤其是硬磁材料在被充磁后可以用于制作双向驱动器，采用一个永磁体和电磁线圈构成的电磁铁即可构成双向的微型电磁驱动器，这可简化微驱动器的结构，充分利用微驱动器中的有限空间。通过改变电磁线圈驱动电流方向在两个磁体之间产生的吸引力和排斥力，可作为双向微驱动器的驱动力。同时，将永磁体制作于微驱动器中，可以减小微驱动器的能耗与发热量。 尽管双向磁驱动器有诸多优点，但传统的磁体制作工艺与微加工艺却不相容，使得电磁驱动微器件的实现比较困难。许多研究者在永磁体的微型化成型制备方面积累了相当多的研究资料。B.Wag-net等人将一个1.5 mm×1.5 mm×1.0 mm的钕铁硼永磁铁粘于硅薄片上制成了微驱动器。W.S.Wang等人用钕铁硼磁粉与硅橡胶相混合制成具有永磁特性的复合柔性膜，并可用于微磁驱动装置。不过，用这些方法获得的永磁体尺寸多是毫米级范围，要想达到真正的微米级器件难度较大。M.Nakano等人用脉冲激光沉积(PLD)法制得了钕铁硼薄膜，但脉冲激光沉积法需要在923～1023 K下进行，这与微加工工艺不兼容。T.M.Linkopoulos等人首先介绍了采用电镀方法制作CoNiMnP永磁体的方法，张博军对用于微驱动器的CoNiMnP永磁阵列进行了探讨。本文作者曾通过大量的实验结果对比，对几种合金电镀液所获得的CoNiMnP永磁薄膜进行了筛选优化。

微驱动器所采用的形变材料有硅、氮化硅、聚酰亚胺。硅和氮化硅的杨氏模量太大，在有限的驱动力作用下产生的偏移小(小于10μm)，不利于在一些偏移要求大的场合使用，比如用作微泵的驱动器，要求振动膜的偏移大、冲程体积大。PDMS的柔性大、其杨氏模量只有750 kPa，能够得到较大的偏移(大于50 μm)。同时，硅橡胶的物理、化学性能均比较稳定，生物兼容性很好，可广范应用于微流控系统中。

　　1 微驱动器的结构

本文所研究的电磁驱动器如图1所示。上下两层结构，上层为内嵌有CoNiMnP永磁体阵列的PDMS振动膜，下层是平面螺旋线圈，上下两层被键合在一起。平面螺旋线圈是铜线圈，采用电镀工艺制作在一个硅片上；在另一块3英时(76mm，(100)面)硅片双面生长2μm厚的氧化层，之后溅射100 nm(Cr20 nm／Cu80 nm)厚的种子层。然后甩正胶AZ4903，转速为1 400r／min，胶厚度为25μm，并在50℃下烘1 h，在90℃下烘2 h。然后，用掩模版进行光刻得到电镀模。电镀之后在硅片另一面甩10 μm厚的正胶AZ4903，烘胶后光刻，显影后在硅片背面开出窗口，采用反应离子刻蚀(RIE，Nextral NE100)方法去掉窗口处的SiO2，剩余的氧化层在湿法刻蚀硅时作为掩膜。在3 000 r／min转速下旋涂PDMS(Rhodia○R硅橡胶本体与固化剂之比为0.7：10)，在90℃下烘1 h，测量PDMS膜的厚度为40～45μm。在湿法刻蚀硅时采用一个塑料模具保护电镀层，湿法刻蚀留约50μm厚的硅，以免碱液渗透破坏振动膜。最后采用反应离子刻蚀法去掉剩下的硅，得到PDMS振动膜。刻蚀时采用CHF3和SF6混合气体，其参数设置：CHF3流量为38 cm3／min，SF6流量为15 cm3／min，压力为30 mT，RF功率为50 W，刻蚀速率约为100 nm／min。然后，采用充磁机将磁体阵列沿竖直方向磁化。本方案中采用磁体阵列而没有采用一整块磁体，是由于磁体阵列可以减少CoNiM-nP电镀层与硅基体之间的应力，同时可以充分利用振动膜的柔性。


　　2 微驱动器的分析

　　2.1 微驱动器的电磁分析

永磁体阵列沿竖直方向磁化后其剩余磁化强度为Br。对于CoNiMnP，磁矫顽力Hc=87.7 kA／m，剩磁强度Br=0.2 T。当给下层的平面螺旋线圈施加电流时，平面螺旋线圈即可看作一个电磁铁，电磁铁产生的磁场对上层的永磁体阵列产生磁力，二者之间的电磁力可以描述为

　　
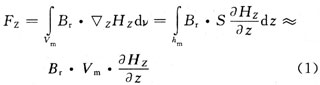
式中：HZ是平线圈磁场的Z向分量；Br是磁体阵列的剩磁强度；S、hm和Vm分别是磁体的表面积、高度和体积。

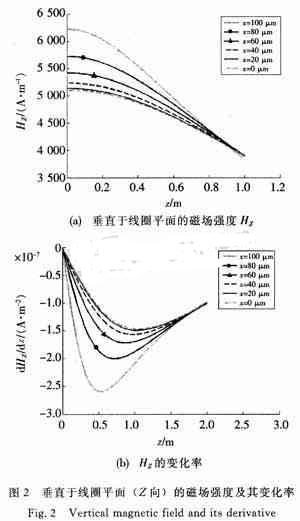
多匝方形线圈产生的磁场相当于每一匝线圈所产生磁场的叠加。利用单匝线圈磁公式，由Matlab软件进行分析，得出图2所示结果。图2(a)是线圈电流为0.3 A时所采用的平面螺旋线圈磁场的Z向分量，图2(b)是线圈磁场Z向分量随高度的变化率。由图2(a)和图2(b)可以看出，随着高度Z的增加，HZ急剧减小，而HZ的变化率存在一个最大值，经分析可知，这个最大值所处的Z值与最里面一匝方形线圈的边长呈线性关系。