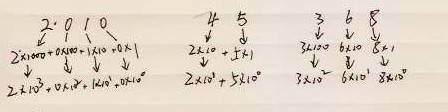电路换算上的二进制数

后再将处理结果根据需要转换为相应的模拟信号输出。从一般的模拟信号到数字信号，要经过采样、 量化、编码，最终一个连续的模拟信号波形就变成了一串离散的、只有高低电平之分"0 1 0 1..."变化的数 字信号。自然界来的，或者通过传感器转化的主要是模拟信号，那么为什么要多此一举把它们变为数字信号 呢？原因有以下几点：

　　一、模拟信号有无穷多种可能的波形，同一个波形稍微变化就成了另一种波形，而数字信号只有两种波 形（高电平和低电平），这就为信号的接收与处理提供了方便。即，数字信号易于传输，抗干扰能力强。

　　二、模拟信号由于它的多变性极容易受到干扰，其中包括来自信道的和电子器件的干扰，模拟器件难以 保证高的精度（如放大器有饱和失真、截止失真、交越失真，集成电路难免有零点漂移）。而数字电路中有 限的波形种类保证了它具有极强的抗干扰性，受扰动的波形只要不超过一定门限总能够通过一些整形电路

（如斯密特门）恢复出来，从而保证了极高的准确性和可信性，而且基于门电路、集成芯片所组成的数字电 路也简单可*、维护调度方便，很适合于信息的处理。特别是计算机科学技术发展后，很多模拟电路无法实 现的功能都可以在采用数字电路来实现。

而电子计算机的出现，让数字电子技术有了更广阔的发展空间，也让我们的生活更加的丰富。手机带 给我们联络的方便，电脑带给我们工作和娱乐以及学习的便利，天上的飞机，路上的汽车，让我们出行更加 方便，家中的空调冰箱洗衣机微波炉等让我们生活更加舒适。在手机、电脑、飞机、汽车以及家电中都有一 块或者多块的微处理器在工作，而这些微处理器就是由数字电路构成的。

2     0 和 1 的舞蹈

2.1      二进制数的来历

电，发明出来是为人类服务的，那么电路同样的是为人们服务的，也就是说我们需要在电路中能够帮 助我们做平时生活中的事情，这些事情应该是我们不用电也可以来做的。举个例子，譬如我们生活中的数， 我们采用的是十进制数，今年是 2010 年，就是指从耶稣诞生之年到现在有 2010 年了，班上有 45 个人， 买了一条裤子花费 368 元等等，那么在这些数字的背后隐藏着什么呢？我们都知道 1+1＝2，但是陈景润花 费了很大的功夫才证明，这说明即使我们看起来很平常的的事情也隐藏着一些我们不知道的因素，在这里我 们不是来讨论 1+1＝2 的，因为我们不是顶极的数学家，但关于十进制数，我们可以讨论一下一些普通人都 有能力理解的东西。2010，45，368 这些数字给我们提供了 2 个信息，数码和数位，2010 由三个数码

0，1，2 构成，45 由两个数码 4，5 构成，368 由三个数码 3，6，8 构成，而且这些数码的位置不一 样，那么他们所代表的大小不一样的，如图 1：

图 1 十进制数的数位、基数和权

图中 10 就是基数，而  103 、 102 、 101 、 100     也就是 1000，100，10，1 就是权。所谓的权，就是在 这个数中占的数值大小。也就是说 2010 中的"2"代表了 2 个"千"，45 中的"4"代表了 4 个"十"，而 368 中 的"8"代表了 8 个"一"，而且同一个数码放在不同的位置上就代表了不同数值，如 555 中，三个 5 的权分别

100，10，1，那么第一个 5 代表的数值就是 5X100，第二个 5 代表的数值是 5X10，的三个 5 代表的数

值是 5X 1。采用这种方法，我们就可以用有限的数码来表示无限的数据了。

总结一下，十进制采用了 0，1，2，3，4，5，6，7，8，9 共 10 个数码，基数是 10，进行运算 的时候，我们采用逢十进一。

这是我们现实生活中需要用到的十进制的一些情况，那么我们在数字电路中必然也要采用这种计数方 法，电路中传输的就是电压和电流，我们要用 10 种不同的状态来表示这 10 个数码有点困难。我们举例来 说吧，譬如有一个电压，0～5V ，那么我们就可以这样来表示 0～9 这 10 个数码，如表 1。

表 1 电压和数码之间的对应关系