理论与实践：随机噪声对时序抖动的影响

 引言

　　时序抖动和时序噪声属于人们了解甚少的工程概念，而它们又是模拟设计和数字设计中最重要的参数。尤其是在高速通信系统中，恶劣的抖动性能会导致更高的误码率，并限制系统速度。时序抖动一般定义为数字信号在某一重要时刻相对于其理想时间位置的短时间偏离。有若干因素会影响随机时序抖动，包括宽带噪声、相位噪声、杂散信号、压摆率、带宽。相位噪声和宽带噪声都是随机的，而杂散信号是由串扰和电源耦合等各种可确定的干扰信号导致的确定性响应。如同本文稍后提到的那样，压摆率和带宽也影响抖动。图1描绘了一条非理想的正弦曲线，它包含了这三种噪声源。图2显示了一个数字信号，伴随的抖动随时间而积累。

　　本文旨在解释和论证时序抖动和这三种噪声源之间的直接关系。

图1. 对时序抖动产生影响的三个噪声源。

　　随机噪声与杂散信号导致的抖动。抖动会随时间积累。

图2. 时钟信号内的随机噪声与杂散信号导致的抖动。抖动会随时间积累。

　　宽带噪声对时序抖动的影响正弦波的抖动

　　所有电子元件都产生宽带噪声，尤其是放大器和逻辑器件。宽带噪声也称作噪声底，是散粒噪声和热噪声的结合。散粒噪声在二极管和晶体管中很常见，是由电荷穿越半导体结的势垒时的随机跳跃导致的。另一方面，热噪声不受电流的影响。它是由载波的随机热运动导致的，例如在MOSFET的栅极和通道阻抗范围内。热噪声功率与阻抗和温度成正比。

　　随着现代元件的工作带宽进入数千兆赫兹范围，宽带噪声对时序抖动的影响变得相当突出。例如，一个宽带放大器驱动器的带宽是40GHz，噪声系数是10dB，小信号增益是20dB，输出功率是0dBm，则它产生的噪声输出是-38dBm （-174dBm + 10dB + 20dB + 10log10（40GHz））。这导致38dB的信噪比（SNR）。在这个SNR水平，宽带噪声就是时序抖动的重要影响因素。总均方根（RMS）噪声电压是噪声底在频带内的积分。图3说明了RMS噪声是如何转化为时序抖动的。

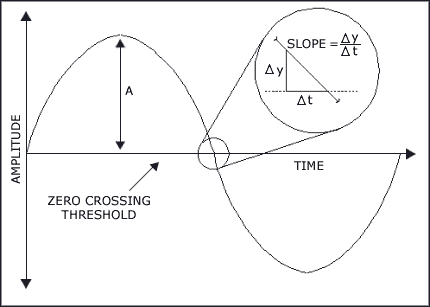
图3. 噪声电压Δy穿越0V，使信号提前Δt达到阈值，从而产生了抖动。

　　从数学上来说，可以用下面的公式表示包含宽带白噪声的正弦波：

其中A为振幅，ω是角频率，vn（t）为时刻t处的噪声电压。随机噪声vn（t）具有高斯（正态）分布。噪声电压ƒ（vn）的概率分布（vn）为：

其中（vnRMS）为RMS噪声电压。为了理解噪声电压是如何转换为时序抖动的，可考虑把y（t）施加到抖动测量仪器（如带直方图功能的采样示波器）的输入端。每次y（t）穿越0V阈值时，直方图上就增加一个数据点。正如图3所示，在时间Δt内，存在噪声信号Δy达到阈值的可能，因此抖动被加到直方图中，时间比预期的采样点早或晚Δt。概率密度为时序抖动Δt的函数，是通过在公式2中设置vn = Δy = Asin（2πƒΔt）来计算的。结果就是抖动分布函数，如直方图所示。

　　假设Δt相比正弦曲线周期而言很小，那么可以对公式3进行简化，得到：Asin（2πƒΔt ≅ A（2πƒΔt = AωΔt。

公式3可变为：

把公式4中各项的分子和分母同除以Aω，得到：

公式5为抖动分布函数，除比例因子1/Aω外，它与公式2中的高斯分布相似，因此，得到的RMS抖动为：

图4所示的测试装置用来验证公式6。纯正弦波信号和宽带噪声信号相互叠加，然后输入采样示波器，它在零交叉处测量抖动。为了确保测试结果有意义，设置的输入宽带噪声要高于示波器的噪声底。图5和图6显示了实验结果。图5表明在RMS噪声恒定时，抖动是频率的函数；图6表明频率恒定时，抖动是RMS噪声的函数。测量得到的抖动曲线和计算得到的抖动曲线之间具有相似性，证明公式6可用来把宽带噪声转化成时序抖动。

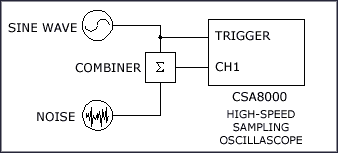
图4. 抖动测试装置#1：噪声和纯正弦波信号叠加。

图5. 在RMS噪声一定的情况下，抖动为频率的函数。

图6. 在频率一定的情况下，抖动为RMS噪声电压的函数。

　　普通波形的抖动

　　经过稍微修改，公式6还能用于其他波形的抖动转化。根据定义，公式6中的A项是0V阈值时的压摆率S。只要已知该阈值处的压摆率，任何波形都可用于求出Δt与Δy之间的关系，这是因为vn = Δy = SΔt （图3）。把它代入公式2得到公式7：

把公式7中各项的分子和分母同除以S，得到：

除比例因子1/S外，公式8与公式2中的高斯分布相似，因此，得到的RMS抖动为：

图4所示的测试装置再次用于验证公式9。正弦波曲线用一个压摆率可变的方波代替。在方波上升沿的50%处测量抖动。图7所示结果表明公式9是正确的。

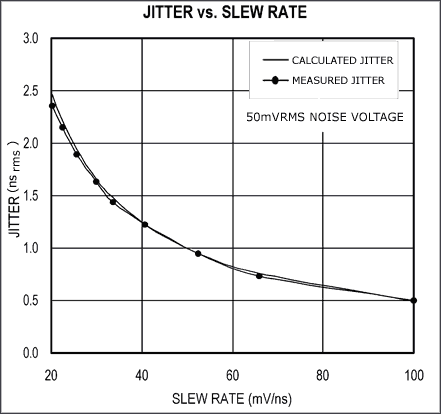
图7. 在方波上升沿的50%处测量抖动。