理论与实践：随机噪声对时序抖动的影响

　　图7中给出的信息引出了一个有趣的现象。似乎波形的压摆率越快，产生的抖动越小。然而，较快的压摆率要求较高的工作带宽，这增加了系统中的RMS噪声。因为RMS噪声与带宽成正比，因此系统设计者必须仔细选择压摆率和带宽，来使抖动降到最低程度。

　　相位噪声对时序抖动的影响相位噪声存在于任何有源元件和无源元件中，但它在振荡器中表现最为严重。这些振荡器包括晶体自激振荡器和时钟恢复应用中的锁相振荡器。相位噪声是一种描述频谱纯度的指标。例如，理想情况下，振荡器输出应该是一条纯正弦曲线，表示为频域中位于某个单一频率的垂线。然而，在现实情况中，振荡器存在一些噪声源，它们会导致输出频率偏离其理想位置，因此在载波（基波）频率附近，产生了一个其他频率的"裙边"效应（图8）。这些频率被称作相位噪声，是由对振荡器进行调制的噪声源引起的。它们的电平通常比噪声底高，频率接近载波频率。相位噪声通常被指定为偏离载波的某个频率处的噪声功率与载波功率之比，在1Hz带宽之内。由于相位噪声来自于噪声源对信号的频率调制，因此相位噪声不受压摆率的影响。

图8. 由于振荡器的噪声频率调制，输出频谱中出现"裙边"效应。

　　受大多数抖动测量设备能力所限，与测量低噪声信号在时域中的抖动相比，通常更容易通过测量它在频域中的相位噪声来确定其纯度。例如，多数抖动测量示波器只能测量低达1psRMS的抖动。大多数实时示波器的带宽仅为7GHz。而另一方面，相位噪声设备能获得目前最佳的低噪声示波器的噪声测量水平（在时域中远小于1ps），并提供高达40GHz的带宽。

　　在早期的文章［1-2］中我们已经探讨了相位噪声和时序抖动的转换问题。为了得到相位噪声与抖动的关系式，可以考虑把公式10作为一个带有相位噪声的正弦曲线：

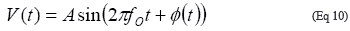
其中A是振幅， fo是额定频率， Φ（t）为相位噪声。通常在两个或多个周期之间的0V交越处测量抖动。在0V交越处， 公式10括号内的各项为2πN：


其中t1为第一个零交越时刻，t2为第N个零交越时刻。两个公式相减得出：

两个交越点之间的时间为周期数量加上抖动：

TO为周期，即1/fO，Δt是N个周期后积累的抖动。把公式14代入公式13得：

重新整理公式15，并消去2πN项，得到抖动：

RMS抖动的平方为：

因为Φ（t）是个稳态过程，所以：

其中SΦ（ƒ）为Φ（t）的频谱密度，f为偏移（傅立叶）频率。公式17的中间项变为：

其中RΦ（τ）是Φ（ƒ）的自相关函数，是经过τ ≅ NTo个周期后的时间。经过N个周期后，在时刻RMS抖动的平方τ为：

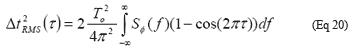
利用代数公式1 - cos（2Φƒτ = 2sin²（Φƒτ）），并假设相位噪声接近载波并且对称（就是从-fOFFSET到0的积分等于0到+fOFFSET的积分），公式20可以重写为：　

SΦ（ƒ）近似等于相位噪声L（ƒ） ［3］；也就是说，傅立叶频偏比载波频偏小得多： fOFFSET 《《 fO。

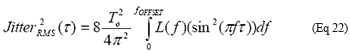
为了验证公式22，使用了一个相位调制电路［4］，它是图9所示测试装置的一部分。相位调制电路可以非常方便地产生无杂散、可变相位噪声信号。首先，利用采样示波器针对时序抖动测量该电路的输出，然后用频谱分析仪（没有画出）针对相位噪声测量其输出。图10显示了该电路的相位噪声图。它类似于锁相振荡器的噪声图，在这种振荡器中，相位噪声在环路带宽内是恒定的，并在带外滚降。图11给出了使用数值积分对公式22求积分后得到的相对于周期的累积抖动。图11中的曲线证实了公式22的正确性。

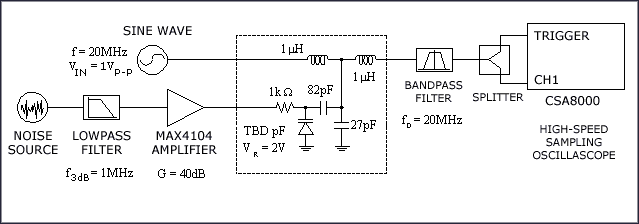
图9. 抖动测试装置#2：使用相位调制器产生相位噪声和抖动。

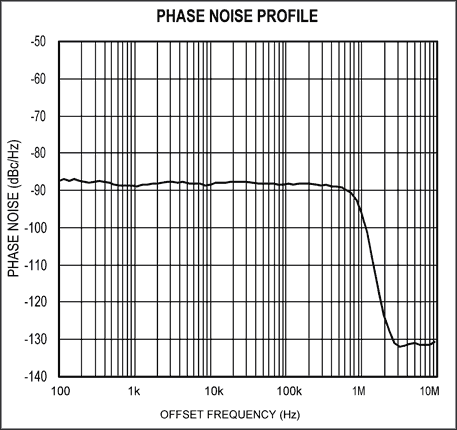
   　图10. 相位调制电路的相位噪声图形。

图11. 图形显示的是相对于周期的累积抖动，证实了公式22的正确性。

　　杂散噪声对时序抖动的影响杂散信号也对时序抖动有影响，尤其是在振荡器中。杂散信号是由锁相环基准的杂散信号、电源耦合、相邻电路的串扰、噪声源引起的。如图1所示，这些杂散信号通常表现为载波频率附近的小尖峰。公式22有助于建立杂散信号和时序抖动的关系。由于杂散只发生在特定频率，因此公式22中的积分函数可以用总和来代替：

同样，τ ≅ NTo为经过N个周期的时间。由于公式23未假定杂散信号是对称的，所以要乘的系数为4而不是8。在计算抖动时，载波两侧的杂散信号都必须包含在内。L（fn）为杂散信号相对于载波（预期信号）的振幅，通常以dBc为单位。fn为n次谐波的频率偏移。图12是公式23的波形图，使用载波两侧的杂散信号，频偏为100kHz，振幅为-40dBc。参考文献1中验证了公式23，方法是用一条正弦波调制一个压控晶体振荡器，产生载波两侧的杂散信号（没有画出）。

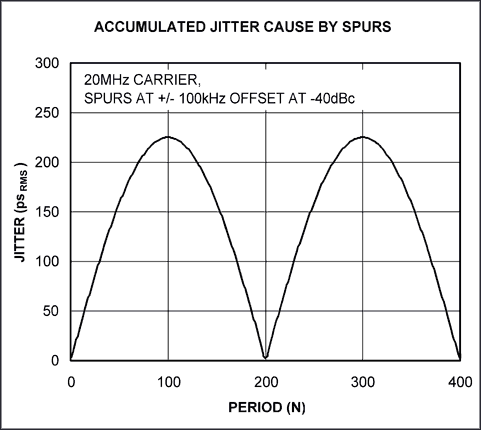
图12. 公式23的曲线，显示了载波两侧产生的杂散信号。