基于瞬时无功电流理论三相谐波提取的DSP实现
引言
有源滤波器是目前国内外谐波抑制技术的一个重要研究方向,在国外APF技术已得到了大量应用。APF技术的原理就是把三相畸变电流的谐波提取出来作为指令电流,控制PWM主电路产生一反向的谐波电流以补偿电网中的谐波电流,因此,三相谐波电流提取的效果直接决定了APF谐波补偿的效果。
1 现有三相谐波检测方法
图1是典型并联结构的APF原理框图。谐波电流的检测方法都是基于非正弦条件下有功功率和无功功率定义而产生的。三相谐波检测的方法很多,从目前的资料看主要有以下几种。
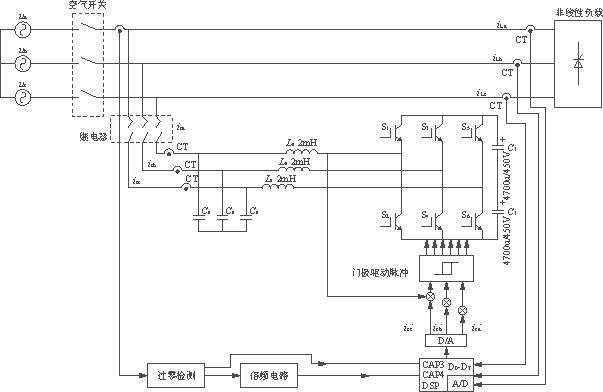
图1 并联结构APF原理框图
1)方法1 采用模拟带通滤波器检测高次谐波电流[1],这种方法的优点是电路结构简单,造价低,输出阻抗低,品质因素容易控制,但是,模拟滤波器的元件容易受外界影响,而且当电网频率发生波动时,实际检测出的谐波电流中含有较多的基波分量。
2)方法2 基于频域分析的FFT[2]和DFT[3]分解方法,这种方法将非正弦的交流电流表达为基波电流和谐波电流之和,然后根据三角变换方法将基波电流进一步分解为无功电流和有功电流。这种方法由于计算很复杂,因而有较大延迟。
3)方法3 基于自适应干扰抵消原理的自适应闭环检测方法[4],这种方法把电压作为参考输入,负载电流作为原始输入,构成一闭环连续调整的谐波及无功电流自适应检测系统,这种方法虽然也是采用模拟电路实现,但是这种检测系统的运行特性基本与元件参数无关。
4)方法4 基于广义瞬时无功功率p,q计算方法,这种方法是目前APF中常用的一种方法,其主要原理框图如图2所示。这种方法是基于瞬时无功功率理论,它先计算出有功功率p和无功功率q,然后经低通滤波器(LPF)得到有功功率和无功功率的直流分量,然后通过功率和电压计算出三相的基波分量。这种方法的一个局限就是只能应用在电网电压无畸变的时候。
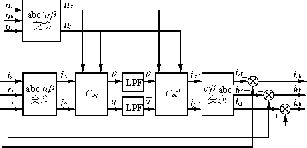
图2 pq运算提取三相谐波的原理框图
5)方法5 基于广义瞬时无功功率电流的计算方法,这种方法也是本文要讨论的谐波提取方法,是方法4在瞬时无功功率理论上进一步扩展的结果,其具体原理将在下面讨论。这种方法的优点就是在电网电压有畸变的情况下,也能够精确地提取谐波电流。
2 基于广义瞬时无功功率电流理论的谐波电流检测方法
瞬时无功功率理论最早于1983年由日本学者Akagi[5]提出来;西安交通大学王兆安教授于1992年进一步深入研究了三相电路瞬时无功功率理论[6],进一步定义了三相电路的瞬时无功功率和各相的无功功率和无功功率电流,研究了广义瞬时无功功率理论和传统理论的关系,从而在理论上为方法4、方法5的谐波提取方法提供了依据。文献[7]及[8]详细地比较研究了这两种谐波电流检测方法,从理论上分析了方法5不受电网电压畸变影响的原因,并仿真研究了这一结论。基于广义瞬时无功功率电流理论的简单阐述就是:无论电网电压畸变与否,三相电流对称与否或者是否畸变,正序三相电流ia,ib,ic经过dq变换后的id,iq可以表示成式(1)的形式。id为d轴电流直流分量,它与负载的基波有功功率相对应;iq为q轴直流分量,它与负载基波相位移无功功率相对应,d轴交流分量、q轴交流分量和O轴分量io与负载基波不对称及高次谐波无功功率相对应。
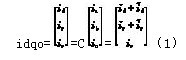
式中:

基于无功功率电流理论,谐波电流检测方法的计算框图如图3所示。从图3不难看出,计算主要分为4个过程。
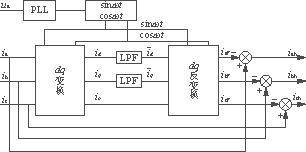
图3 dq变换提取三相谐波的原理框图
1)dqo变换,将abc坐标系的三相电流转换到dqo坐标系;
2)低通滤波,将id,iq中的直流分量id,iq分别滤出来;
3)dqo/abc变换,将id,iq转换成abc坐标系下的基波电流iaf、ibf、icf;
4)提取谐波。
其计算公式如式(2)所示。
iih=ii-iif(2)
式中:i表示a,b,c相。
3 低通滤波器的设计
从上面的分析不难看出,基于广义瞬时无功功率电流谐波检测方法的效果主要还是取决于低通滤波器的设计。
3.1 数字滤波器种类的选择和模拟滤波器原型的选择
无限响应滤波器的特点就是实现同等要求的数字滤波器阶数要比有限响应滤波器低很多,一般关系[9]是1/5~1/10,而且无限响应滤波器设计有现成的闭合公式、数据和表格,因此计算量小很多。有限响应滤波器有严格的线性相移,因此稳定性比无限响应滤波器要好。根据APF的要求,数字滤波器要滤除的是直流分量,因此可以不考虑相移;另外为了缩减DSP运算时间宜选用无限响应滤波器。
模拟滤波器目前主要有Butterworth、Eliptic、Chebychev、Bessel等几种。从幅频特性曲线可知,当截止频率较低时,Butterworth检测精度最高,这是因为它的频率特性在零点附近最好;如果截止频率增大一些Elliptic滤波器的精度最好,Chebychev滤波器次之,Butterworth稍差一点,Bessel滤波器最差。而Bessel滤波器动态相应过程最快,依次是Butterworth, Chebychev, Ellipitic。考虑到系统的稳定性,Butterworth Chebychev,Ellipitic,Bessel依次递减。因此本文采用的是Chebychev。
3.2 采样频率fs和截止频率fc
采样频率过高则对低频处理精度影响较大,因为采样频率过高则低通滤波器运算时对字长的要求很高;采样频率过低则对高于采样频率一半频率段进行采样时会采到低频错误信号。APF对电网谐波提取主要考虑5次、7次、11次和13次,13次信号的频率为650Hz,本次采样频率选择1500Hz。
截止频率fc越小,谐波电流的检测精度越高,但动态响应过程太慢,截止频率fc越大,可以加快动态响应过程,但由于低次谐波未被LPF衰减掉,容易造成检测波形失真,影响检测精度。APF中电流最低次谐波为5次,经dq变换后为4次即200Hz。综合考虑截止频率选用130Hz。
最后用归一化滤波器计算得传递函数为:
H(z)=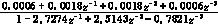
- 通用和低噪声的有源滤波器提供达10MHz的可重复性能(01-05)
- 混合有源电力滤波器的仿真研究(08-03)
- 电网有源滤波器结构及其应用(05-27)
- 直流侧电力有源滤波器滤除谐波干扰的原理及方案(05-01)
- 关于多级低通有源滤波器的增益及Q值排序的深入思考(03-16)
- 灰色预测控制在有源滤波器中的设计应用(04-01)
