水声信号功率放大器的设计与实现

在现代主动声纳系统中，往往需要针对不同背景噪音以及不同的要求，适时地选择信号波形，工作频率，信号时间宽度，带宽等。例如，常用的信号有单频矩形脉冲(CW)，线性调频脉冲信号(LFM)，双曲线调频信号等。不同的信号具有不同的特性。对于相同的多普勒分辨率，LFM脉冲的试验分辨能力要高于CW脉冲，而对于相同的时延分辨力，LFM则要高于CW脉冲。当目标多普勒频移较小时，相对于长CW脉冲而言，LFM脉冲具有较小的模糊面积，受到少一些的混响影响，而当目标多普勒增大时，长CW脉冲比LFM脉冲信号抗混响效果要好。

本文所提到的水声信号发生系统采用多功能的数据采集接口板作为信号源，可以通过编写程序方便产生所需的信号。其所产生的信号稳定，精度高，并且修改容易，通用性强。但由于要直接产生满足要求的正弦信号具有很大难度，所以产生的都是矩形信号，而且信号的幅度、功率均很小。为解决这一问题，这里提出了功率放大电路，将数据采集接口板产生的矩形信号转换为正弦信号，并进行幅度和功率放大，以满足换能器对信号的要求。

1 总体设计

由式(3)可以得出以下结论：周期信号的傅氏变换在各谐波频率处是一个无限长的等间距的冲击序列。周期函数具有离散的傅氏变换频谱。如能设计一电路将矩形周期信号的基频谐波分量分离出来，便达到了将矩形周期信号转换为正弦信号的目的。图1为系统总体框图。

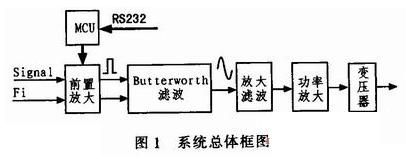
由于上级电路产生的矩形信号幅度很小，所以先通过前置放大模块进行初步幅度放大和滤波。前置放大模块的放大增益可控。PC机通过RS232接口与单片机通信，单片机接收到PC机发出的信息后，再通过调整电阻网络调整增益。这样整个系统最终的输出信号幅度便可以通过PC机控制。矩形信号经过巴特沃思滤波器滤波后转换为正弦信号，再经过放大滤波，便可传给大功率运放转换为大功率信号。最后通过变压器驱动换能器以产生声信号。

2 电路设计

该电路按如前所述的功能，可以将其划分为串口通信模块、前置放大模块、巴特沃思低通滤波模块以及大功率运放模块。

2．1 串口通信模块

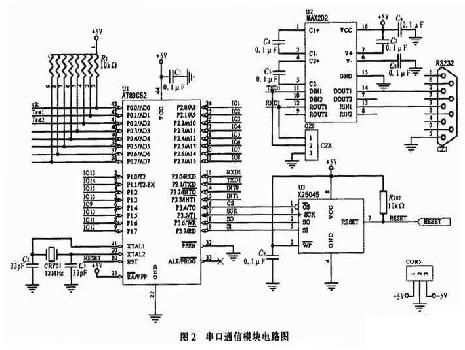
系统通过标准RS232接口与PC机进行通信。该串口通信模块的核心是单片机AT89C52，其带有一个UART(通用异步收发器)。用UART实现串口通信非常容易，其收发协议与标准RS232接口是一致的，只是在电气特性上有差异：UART采用的是CMOS电平，而RS232接口则采用RS232电平。因此该电路采用了MAX202电平转换器来转换电平。其电路图如图2所示。

在现代主动声纳系统中，往往需要针对不同背景噪音以及不同的要求，适时地选择信号波形，工作频率，信号时间宽度，带宽等。例如，常用的信号有单频矩形脉冲(CW)，线性调频脉冲信号(LFM)，双曲线调频信号等。不同的信号具有不同的特性。对于相同的多普勒分辨率，LFM脉冲的试验分辨能力要高于CW脉冲，而对于相同的时延分辨力，LFM则要高于CW脉冲。当目标多普勒频移较小时，相对于长CW脉冲而言，LFM脉冲具有较小的模糊面积，受到少一些的混响影响，而当目标多普勒增大时，长CW脉冲比LFM脉冲信号抗混响效果要好。

本文所提到的水声信号发生系统采用多功能的数据采集接口板作为信号源，可以通过编写程序方便产生所需的信号。其所产生的信号稳定，精度高，并且修改容易，通用性强。但由于要直接产生满足要求的正弦信号具有很大难度，所以产生的都是矩形信号，而且信号的幅度、功率均很小。为解决这一问题，这里提出了功率放大电路，将数据采集接口板产生的矩形信号转换为正弦信号，并进行幅度和功率放大，以满足换能器对信号的要求。

1 总体设计

由式(3)可以得出以下结论：周期信号的傅氏变换在各谐波频率处是一个无限长的等间距的冲击序列。周期函数具有离散的傅氏变换频谱。如能设计一电路将矩形周期信号的基频谐波分量分离出来，便达到了将矩形周期信号转换为正弦信号的目的。图1为系统总体框图。

由于上级电路产生的矩形信号幅度很小，所以先通过前置放大模块进行初步幅度放大和滤波。前置放大模块的放大增益可控。PC机通过RS232接口与单片机通信，单片机接收到PC机发出的信息后，再通过调整电阻网络调整增益。这样整个系统最终的输出信号幅度便可以通过PC机控制。矩形信号经过巴特沃思滤波器滤波后转换为正弦信号，再经过放大滤波，便可传给大功率运放转换为大功率信号。最后通过变压器驱动换能器以产生声信号。

2 电路设计

该电路按如前所述的功能，可以将其划分为串口通信模块、前置放大模块、巴特沃思低通滤波模块以及大功率运放模块。