低频正弦波形发生器仿真与设计

利用核磁共振方法勘查地下水就是利用一个铺在地面上的线圈发射并接受NMR信号，线圈中需通入某一谐振频率（拉莫尔频率即氢质子在地磁场中的旋进频率）的正弦波作为激发源。欲获得合适的正弦波，分析了谐振电路的频率特性，对低频正弦波形发生器进行仿真，得到相应的仿真结果，从而设计了实际发射电路，并通过室内实验获得与仿真电路一致的结果，解决了将直流电源能量转化为交流能量发射的实际需要。该正弦波形发生器优点在于发射波形没有衰减，且发射电流持续时间可调节。

1引言

在核磁共振（ NMR）测深工作中需要发射某一频率的正弦波作为激发源，这一频率与地磁场大小满足一定的关系，如式（1）。NMR测深中认为地磁场B₀是均匀的，地磁场强度决定了拉莫尔频率，即激发电流的频率。由激发电流建立激发磁场作为一次场，激发场的强度用激发脉冲矩q= I₀τ_p表示。当激发电流断开后，用同一天线（发射/接收）接收由于二次场（弛豫磁场）变化而在接收天线中产生的感应电动势（即NMR信号）的弛豫场。在稳定地磁场B₀（地磁场）作用下，具有一定磁矩的氢核绕外磁场运动，运动频率由拉摩尔方程决定：

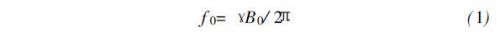
式中： f₀为拉摩尔频率； γ为旋磁比。

根据实测的地磁场强度B₀，就可由式（ 1）求出水中质子的运动频率（拉摩尔频率）

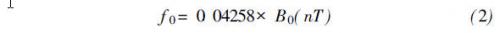
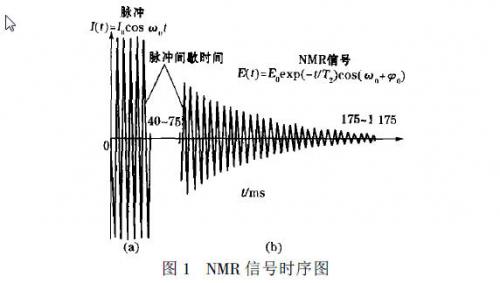
理论上流过天线的交变电流脉冲的包络线为矩形，如图1（a）所示。其中： 1≤t≤τ_p ；ω₀= 2πf₀； I₀ ，S_p分别为交变电流脉冲的幅度和持续时间。发射电流的幅度与持续时间的乘积（ q = I ₀τ_p ）决定了勘探深度，图1（ b）为天线上接收到的NMR信号，该信号按指数规律衰减。

实际工作中需要利用直流电源能量转化为交流能源作为激发场，为获得合适的发射电流，对发射电路进行了仿真设计。

2谐振发射单元的设计

选频电路可以得到合适的正弦波输出。选频电路按功能可分为低通滤波电路、带通滤波电路、高通滤波电路、带阻滤波电路等；按原理可分为谐振式选频电路、集中选频电路、陶瓷滤波器、声表面波滤波器、晶体滤波器等。该发射电路采用谐振式选频电路。在电路中，信号本身不是单一频率的信号，而是占有一定频带宽度的频谱信号，这就要求选频电路的通频带宽度应与它所传输信号有效频谱宽度相适应，为不引入信号的幅度失真，理想的选频电路的通频带内的幅频特性H(f)应满足：

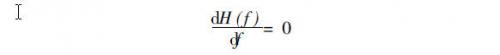
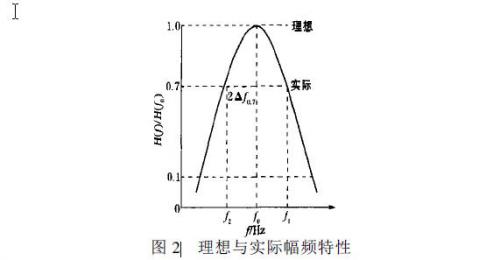
为抑制通频带外的干扰，选频电路通频带外的幅频特性H(f)应满足H(f)= 0.显然理想的幅频特性应是矩形，实际的幅频特性接近矩形，图2的纵坐标是： α(f)= H(f)/ H (f₀)，接近的程度与选频电路本身结构形式有关，通常用矩形系数K表示，定义为：

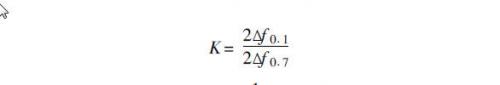
式中： 2Δf_0.7为α(f)由1下降到1/√2时，两边界频率f₁与f₂之间的频带宽度，称为通频带，用B表示， B = f₁- f₂= 2Δf_0.72Δf_0.1为α(f)下降到0.1处频带宽度，理想值K=1，实际值均大于1.

信号通过选频电路，为不引入信号失真，要求在同通频带范围内相频特性应满足：

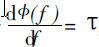
即信号有效频带宽度之内的各频率分量通过选频电路之后，都延迟一个相同的时间，这样保证输出信号中各频率分量之间的相对关系与输入信号完全相同。

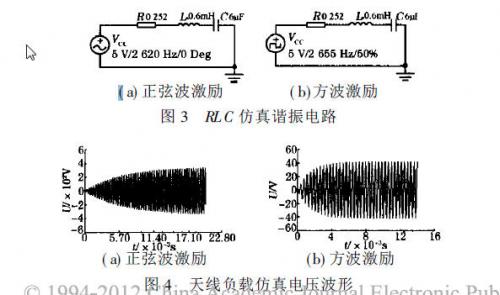
欲获得频率为当地拉莫尔频率的交变电流，且脉冲幅度足够大，可以采用谐振电路来实现， RLC串联谐振电路如图3所示,R,L为电感线圈内阻和电感， C为回路电容， V_CC为外加电动势。由图3可知回路阻抗为

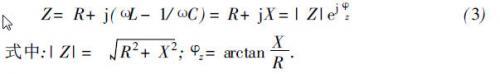
若使激励源角频率等于回路谐振角频率时，即ω= ω₀= 2πf₀= 1/√LC ，此时|Z| = R， |Z|为最小值，回路呈纯电阻性，ψz= 0，回路电流达到最大。回路中的谐振角频率决定于回路本身参数，与激励源无关，图3是采用两种激励源（正弦波和方波）所构成的谐振电路，用仿真测试到的线圈两端电压波形如图4所示，理论计算出回路的品质因数Q= ω.即为ω.L/ R = 50.当回路谐振频率f₀一定时，通频带2Δf_0.7与Q成反比，即：2Δf₀= f₀/Q1在正弦波激励下，图4（ a）的Q大约为60，与理论计算数值基本相符，在方波激励下，图4（b）的Q大约为8.通过仿真可知：在LC串联电路中采用方波驱动时线圈负载也可获得谐振电压波形。那么合适的方波信号是从开关电源获得的，开关电源所提供的电压增大，负载上即可获得更大的电流。实际工作中采用直流电源供电，因此利用方波激励以获得谐振输出电流或电压波形。

（开关电源中利用的开关管要工作在开关状态下，实际工作中开关从开通到关断瞬间会出现反向过冲，易损坏开关，因此实际谐振电路如图5所示