由DAC谐波频谱成分重构其传递函数

谐波（基波）的幅值，M2是2次谐波的幅值，依此类推至MH。谐波幅值通常用相对于基波幅值的分贝数(dBc)来衡量。dBc转换为线性单位的公式如下：

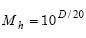
其中D表示测得的谐波幅值，单位为dBc。例如，如果3次谐波的幅值为–40 dBc，则线性幅值M3＝10–40/20或0.01。M1始终等于1，因为根据定义，基波的幅值为0 dBc。

第二步：重构DAC传递函数

该过程的第二步涉及到将谐波测量结果与传递函数相关。f(x)上的点取决于g(t)和u(t)上对应点之间的关系，因此首先必须将频域中的谐波幅值转换到时域。请注意，组成g(t)的DAC码与g(t)正弦形式的相关时间点一一对应。因此，构成g(t)的DAC码与时域相关。此外，u(t)通过f(x)与g(t)相关，而g(t)是一个时域函数，因此u(t)也必须表示为时域函数。这样就能将g(t)中的各时间点tk链接到u(t)中的相关时间点，从而由g(t)和u(t)确定f(x)。

将谐波幅值转换到时域非常困难，因为f(x)必须明确与g(t)中的各可能DAC码（0至2N–1）相关。g(t)是一个理想正弦波，因此确保唯一性的唯一方法是将范围限制在该正弦波单调增加的位置，如图3加粗部分所示。如果没有这一限制条件，f(x)上的一个点可能会映射到g(t)上的两个点，从而导致不明确。

为演示这种不定性，请想象将区间T向下移动。现在，f(x)上的点(xk, fkxk))可以与g(t)上的两个点相关，这是不可接受的。将范围T限制在图中所示位置，将不存在不定性。g(t)为正弦波，因此所需范围T对应于1/2周期，其初始相位偏移为3π/2弧度。

图3. f(x)与g(t)之间的关系

g(t)的范围受T限制意味着u(t)也具有类似的范围限制。因此，将所记录的谐波幅值转换到时域时，必须确保将u(t)限制在与g(t)相同的范围T，如图4所示。

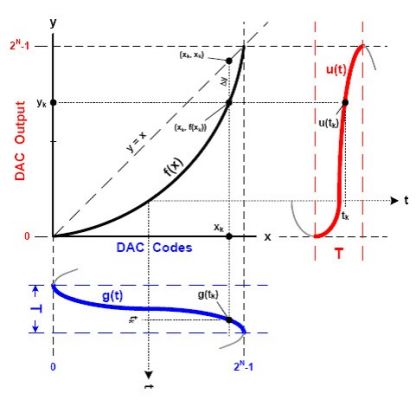
图4. g(t)和u(t)的时域范围

请注意，实际的时间范围T无关紧要，因为f(x)仅在g(t)和u(t)二者的幅值之间起转换作用。为简化分析，将基波频率(f0)归一化为1。因此，2次谐波的频率为2，3次谐波的频率为3，如此类推。所以，谐波频率与谐波数(h)相等：fh=h。这一便捷关系可简化从谐波测量结果Mh创建u(t)的数学计算。

正弦波的一般时域表达式为：

其中β为峰值振幅，θ为初始相位偏移。

用h代替f，并用Mh代替β，可以获得各谐波uh(t)的时域表达式。不过应记住，g(t)偏移3π/2弧度。此外，g(t)与u(t)之间通过f(x)关联意味着g(t)和u(t)在相位上是对准的。用3π/2代替θ可提供所需的对准。下式中，请注意0 ≤t < 1且π取代了2π，目的是将基波限制在范围T所表示的半个周期：

利用各谐波uh(t)的时域表达式，便可以重构复合输出u(t)，表示为基波和谐波信号的和：

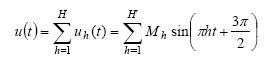
如前所述，我们的目标是将g(t)与u(t)相关以重构DAC传递函数f(x)。此外，g(t)必须恰好由2N个样本组成，以便与f(x)上的点一一对应。因此，g(t)的样本计算公式为：

(n=0,1,2,3 .. 2N–1)

g(t)由2N个样本组成，因此由包括2N个采样的u(t)采样值集重构f(x)似乎是合理的。然而，事实却是至少需要2N+3个采样才能为较小的Mh值提供适当的精度。这种情况下，u(t)各采样点的计算公式应如下：

(n=0,1,2,3 .. 2N+3– 1)

请注意，这将导致u(t)所含的采样数多于g(t)，u(t)的多个样本可能与f(x)和g(t)上的一个点对应，从而使u(t)和g(t)到f(x)的映射关系复杂化。因此，必须对特定的样本组求平均值，以便提供到f(x)的合理映射。下面的伪代码反映了所需的映射关系，其中假设使用一个N位DAC，g(t)有2N个点，u(t)有2N+3个点。阵列DacXfr含有2N个元素，初始值均为0。执行该代码后，阵列DacXfr的元素包含归一化的DAC传递函数。

验证

为验证本文所述的方法，使用一台频谱分析仪来测量一个14位DAC的输出；该DAC由一个代表理想正弦波的输入序列驱动。记录了前14次谐波的幅值（2次到15次，单位dBc），并利用这些值重构DAC传递函数f(x)。然后，将理想正弦输入序列g(t)代入重构的DAC传递函数f(x)进行模拟，产生一个输出序列。一个FFT将u(t)转换为频域等效值U(ω)。从U(ω)提取谐波幅值，并将其与频谱分析仪的测量结果相比较，如表1所示。请注意，与7次谐波相关的最大误差仅为0.065 dB。

由于比例关系，重构传递函数的图形呈现为一条直线(y＝x)。事实上，该传递函数与y＝x的偏差足以产生表1所示的谐波成分。为帮助理解，图5仅显示了该传递函数与理想直线的偏差。垂直轴的单位为LSB。

图5. DAC传递函数的残差