全数字锁相环的设计及分析
时间：03-01
来源：21IC
点击：
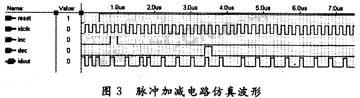
3.3全数字锁相环的实现与仿真
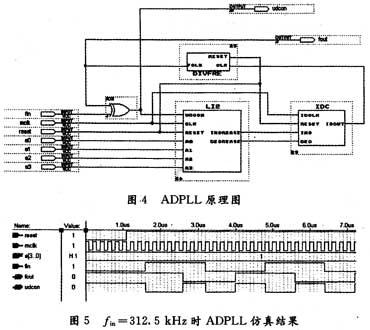
将环路各个模块连接起来完成ADPLL的设计。为了简化设计，将K变模可逆计数器的时钟Mclk与脉冲加减电路时钟2Nclk接在一起，fin等于环路中心频率fc，fc=312.5 kHz。取M=16，N=8，Mclk=5 MHz。当a[3..0]=1时，设定K值为4。为了便于观察，将K变模可逆计数器的输入信号udcon引出。
环路在进入锁定状态后，udcon为占空比为50％的方波。系统原理图和仿真波形分别如图4，图5所示。
由
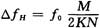可得ADPLL的同步带理论值为：f0／4，即234.375～390.625 kHz。根据仿真实验结果，可以实现稳定锁相的频率范围为：250～357.14 kHz，略小于理论值范围。 4 全数字锁相环数学模型的建立与分析
结合模拟和数字锁相的理论分析，可以得到全数字锁相环的相位和相差传递函数。图6为全数字锁相环的数学模型。
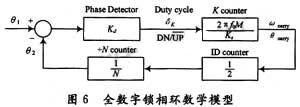
鉴相器可以看作增益为Kd的模块，输出占空比因子δk作为K变模计数器的输入DN／UP，控制"UP COUNTER"和"DOWN COUNTER"的动作。
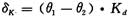
对于异或门鉴相器，相差等于π／2时，δk=1，相差等于-π／2时，δk=-1。因此对于异或门鉴相器增益Kd=2／π，同理可得边沿控制鉴相器增益Kd=1／π。
K变模计数器产生CARRY信号的频率为(f0为环路的中心频率)：
对于K变模计数器，其输入输出信号分别为δk和θcarry，对应的Laplace变换为δk(s)和θcarry(s)，所以K变模计数器的相位传递函数为：
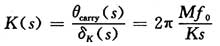
对于脉冲加减电路，由于每个CARRY脉冲使其输出IDOUT增加1／2个周期，可以将他看作增益为1／2的模块。除N计数器可以看作增益为1／N的模块。系统的相位传递函数H(s)表示为：
为了获得最小波纹，对于异或门(XOR)鉴相器和边沿控制鉴相器(ECPD)，K模值分别取为M／4和M／2，相应的时间常数分别为：τ(EXOR)= (N／8)T0，τ(ECPD)=(N／2)T0，其中T0=1／f0。由此可见，N越小，ADPLL的稳定时间越短。在本文中设计的锁相环，Kd=2／π，M=16，N=8，K=M／4=4，代入时间常数公式可得：τ=T0。
5 结 语
本文介绍了一种一阶ADPLL的设计方法，利用VHDL语言完成系统设计和仿真。ADPLL中可逆计数器的模值可以随意改变，用来控制ADPLL的跟踪补偿和锁定时间。除N计数器的分频值也可随意改变，使ADPLL可以跟踪不同中心频率的输入信号。设计好的ADPLL模块还可以作为可重用的IP核，应用于其他设计。同时，在理论分析的基础上，建立了全数字锁相环的一阶数学模型，从而可以根据具体的设计要求定量的计算参数，简化了ADPLL的设计。
- 采用CPLD/FPGA的VHDL语言电路优化原理设计(03-18)