3非连续运行模式的分析
3.1电路说明
非连续运行模式是指二极管D10的瞬态电流iD10在t=t1=[k+(1-k)m]T时下降到零。式中kT<1。
m=1/ξ=M2/k(3R/2fL)(34)
从方程式(34)中我们能看到,非连续模式是由下列因素造成的:
(1)开关频率f太低;
(2)导通占空比k太小;
(3)电感L太小;
(4)负载电阻R太大。
为了分析电路的工作过程,我们把电流和电压变化量放大后的波形显示在图3和图4上。开关闭合和断开状态的等效电路如图2所示。因为电感电流iL11=iL =iL13=iL14在t=t1时,iL=iL11=0,所以VL11-off=VL13-off=VL14-off=kVI/(1-k)m(35)
电感电流iL11在开关闭合t=0到kT期间增加,在开关关断t=kT到t1,即到(1-k)mT期间减小。加于电感L11两端对应的电压分别是VI和 (VO-3VI-VL13-off-VL14-off),因此,kTVI=(1-k)mT(VO-3VI-VL13-off-VL14-off)因而, VO=3VI[1+k/(1-k)m](36)
3.2输出电压Vo的绝对值和负载R电阻之间的关系
方程(30)给出连续模式和非连续模式之间的边界条件。我们把M=3/(1-k)代入方程(34)求出m,再代入方程(36),就能求出输出电压的绝对值和负载电阻之间的关系是:
VO=3VI[1+k/(1-k)m]
=VI[3+k2(1-k)R/2fL](37)
在VI=24V,f=50kHz,L=600μH,R=20Ω~20kΩ条件下进行的实验和分析验证了这一结果。输出电压和负载电阻之间的关系如图8所示。由方程(32)计算出的连续模式和非连续模式之间的边界电阻阻值,在k=0.3时,为R=1224Ω;k=0.6时,为R=1875Ω;k=0.8 时,为R=5625Ω。当负输出罗氏三举变换器的负载电阻阻值大于边界电阻阻值时,变换器工作在非连续模式,此时的输出电压值需用方程(36)进行计算。当负输出罗氏三举变换器的负载电阻阻值小于或等于边界电阻阻值时,变换器工作在连续模式,此时的输出电压值用方程(1)进行计算即可。图8中实线表示计算出的输出电压值的绝对值,虚线表示相应的测量值。因为所有元器件都是非理想元器件,所以测量数据比理论计算值低。由图8可见,当负输出罗氏三举变换器工作在连续模式时,其输出电压绝对值仅取决于导通占空比k的大小,与负载电阻阻值大小无关。此时负输出罗氏三举变换器的输出相当于恒压源。而在非连续模式时,其输出电压绝对值不仅与导通占空比k的大小有关,而且还和负载电阻阻值的大小有关,随其增加而增加。因此为了防止负载开路时其输出电压值过高,超出电容 C11和C10的耐压值而把电容击穿,就需在负输出罗氏三举变换器的输出端接一固定电阻作为死负载。但此电阻的阻值也不宜取得太小,否则会使负输出罗氏三举变换器的功率转换效率降低很多。
 |
| 图8输出电压和负载电阻之间的关系 |
(实线表示计算值虚线表示测量值)
4稳定性分析
对任一变换器电路进行稳定性分析都是至关重要的。根据电路网络和控制系统理论可知,一个系统的稳定性可以根据传递函数极点在s平面上的位置来判定。从图9所示的负输出罗氏三举变换器在开关闭合状态时对变化量的等效电路中,可获得开关闭合状态时的传递函数是:(38)
| 
|
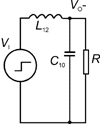
| 图9负输出罗氏三举变换器在开关闭合时的等效电路 |
式中s是拉普拉斯算子。从方程(38)可以看出,负输出罗氏三举变换器在开关闭合状态时是二阶控制电路。
根据Routh判据,在方程(38)的分母多项式中:a2=L12C10R;a1=L12;a0=R。由此可以看出全部系数a0,a1,a2都是正值。所以负输出三举变换器在开关闭合时,整个系统是稳定的。
对方程(38)式中的分子和分母同除以R。当电阻R的阻值趋向无穷大时,方程式(38)又可写为:(39)
所以在开关闭合状态,当负载电阻阻值趋向无穷大时,落在虚轴上的一对虚数极点是:(40)
式中ωn=(L12C10)-1/2是负输出罗氏三举变换器的标称角频率。
当负载电阻阻值不是无穷大时,从方程式(38)可得出其极点的轨迹都在s复平面的左半部分,所以负输出罗氏三举变换器在开关闭合状态时是稳定的。
为了从图10所示的负输出罗氏三举变换器在开关关断状态时对变化量的等效电路中,方便地求出开关关断状态的传递函数,我们对图10电路各部分分别用一些符号来表示,设:
Z1=(1/sC10)∥R=R/(1+sC10R);
Z2=(1/sC11)∥(sL12+Z1)≈1/sC11;
C12=C13=C14=C;L13=L14=L;L12=2L;
C11=C10=C/10。在电感L11两端加一阶跃函数ΔvI就可求出其输出响应和开关关断状态的传递函数:
根据Routh判据,方程(41)的分母多项式中:a4=2C2L2R;a3=20CL2;a2=23CLR;a1=130L;a0=65R;b1=10LCR;c1=0;d1=b2=a0=65R。


