负输出罗氏变换器实用性剖析

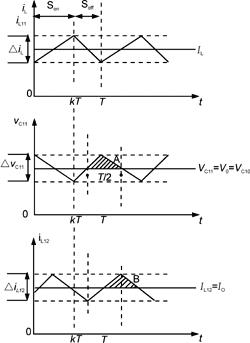
图3负输出罗氏三举变换器理想的电流和电压波形图
(i)VI/L11
(ii)kVI/(1-k)L11
(iii)3[VI/L11+δ'(t)]
(iV))kVI/(1-k)L11
(v)VI/L11+δ'(t)
(a)连续模式
(b)非连续模式

如果流过二极管D10的下降电流iD10在开关再次转向闭合前已下降到零,则电路工作在图2(c)所示的非连续模式工作状态,相应的波形如图3(b)和图4(b)所示。
 |
| 图4负输出罗氏三举变换器理想的电压波形图 (a)连续模式(b)非连续模式 |
负输出罗氏三举变换器的分析是在下列假设下进行的:
(1)负输出罗氏三举变换器的所有元器件都是理想的;
(2)所有电容的容量足够大。因此,电容上电压是一恒定值,并等于VO或VI。在此假设下,在图2所示的等效电路中,电容C10和C11可用电压源VO来代替,电容C12、C13和C14可用电压源VI来代替。
2连续工作模式的稳态分析
2.1电流和电压的平均值
计算过程省略。
连续模式时电压传输增益M为:
M=VO/VI=3/(1-k)(1)
M对k的关系曲线如图6所示,可见M随k的增加而增大。
 |
| 图6电压传输增益M对k的关系曲线 |
负输出罗氏三举变换器电流和电压的平均值如下:
VC11=VO=VC10=MVI
VD10=kVO
VD11=VD12=VD13=VD22=VD23=VD21=VC12=VC13
=VC14=Vs=VI
VL11=VL12=VL13=VL14=0
IL11=IL13=IL14=IL=IO/(1-k)=II/3
IL12=IO=II/M
IS=II
IC10=IC11=IC12=IC13=IC14=0
2.2电流和电压的峰值
从前面图3、图4和图5的分析中,可得出电流和电压的峰值为:
IL11M=IL13M=IL14M=II/3+kTV1/2L11
IL12M=IO+△iL12/2=Io+kIo/16f2C11L12
I1M=ISM=IL11M+IL13M+3δ′(t)+IL14M=3(II/3+kTVI/2L11)+3δ'(t)ID10M=IL11M=II/3+kTVI/2L11
IC12M=IC13M=IC14M=II/3+kTVI/2L11
VD10M=VO
VSM=VD21M=VL11-off+VI=VI/(1-k)
VD11M=VI/(1-k)
VD12M=2VI/(1-k)
VD13M=3VI/(1-k)
VD22M=VI/(1-k)
VD23M=2VI/(1-k)
2.3电流和电压的瞬时值
电流和电压的瞬时值是:(2)(3)(4)(5)(6)(7)(9)(10)(11)
2式中:
iL11(0)=II/3-kVI/2fL11iL11(kT)=II/3+kVI/2fL11(12)
iL13(0)=II/3-kVI/2fL13iL13(kT)=II/3+kVI/2fL13(13)
iL14(0)=II/3-kVI/2fL14iL14(kT)=II/3+kVI/2fL14(14)(15)(16)(17)(18)(19)(20)
2.4电流和电压的变化率
计算过程省略。
电感电流iL11的变化率是:
ξ1=(△iL11/2)/IL11=kTVI/2L11IL11=3VIk/2IIL11f=3kR/2M2fL11(21)
电感电流iL13的变化率是:
ξ2=(△iL13/2)/IL13=kTVI(1-k)/2L13IO=3Rk/2M2fL13(22)
电感电流iL14的变化率是:
ξ3=(△iL14/2)/IL14=kTVI(1-k)/2L13IO=3Rk/2M2fL14(23)
电感电流iL12的变化率是:
ξ4=(△iL12/2)/IL12=k/16f2C11L12(24)
电压vC11的变化率是:
ρ=(△vC11/2)/VC11=kTIO/2C11VO=k/2fC11R(25)
电压vC14变化率是:
σ1=(△vC14/2)/VC14=IO/2fC14VI=M/2fC14R(26)
电压vC13的变化率是:
σ2=(△vC13/2)/VC13=IO/2fC13VI=M/2fC13R(27)
电压vC12的变化率是:
σ3=(△vC12/2)/VC12=IO/2fC12VI=M/2fC12R(28)
输出电压vO=vC10的变化率是:
ε=(△vO/2)/VO=kIO/128f3C11C10L12VO=k/128C11C10L12R(29)
假设:f= 50kHz、L12=200μH,电容C12=C13=C14=C11=C10=10μF,R=10Ω、k= 0.5和电感L11=L13=L14=100μH,我们可得:M=6,ξ1=ξ2=ξ3=0.042,ξ4=0.0125,ρ=0.05,σ1=σ2= σ3=0.6,ε=0.000156。
由此可见,输出电压VO只有非常小的纹波,几乎是理想的直流电压。因为负载是电阻,所以输出电流iO(t)的纹波也非常小,几乎也是理想的直流波形,其数值为IO=VO/R。
2.5连续模式和非连续模式之间的边界
边界方程为:(30)
式中R/fL11是标称负载。要使变换器工作在连续模式,则必须(31)
负输出罗氏三举变换器的电压传输增益M和标称负载R/fL11之间的关系曲线如图7所示。
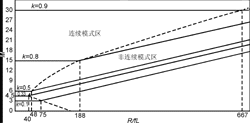 |
| 图7各种k值下电压传输增益M和标称负载R/fL11之间的关系曲线 |
2.6连续模式要求的最小电感值
方程(31)给出了选择工作在连续模式所要求的最小电感值,即:max(32)
通常,选2L11min=L13=L14=L12=L11,变量k和R应在其允许取值范围内选最大值。通常选大的电感量可以减少电感电流变化量,使ξ1、ξ2、ξ3和ξ4远小于1,并使电感电流保持连续。但电感量也不宜取过大,否则会使电感体积增大,影响功率密度值。
为了保持电容上电压的小变化量,所有电容的容量都应选足够大。通常输出电压的变化量要求小于0.01,据此就可从程(29)求出C10=C11所需的最小电容量为:(33)
其它电容也可选此电容量,不过电压的变化量会高一些。为了减少电压变化量,除选C10=C11外,其它电容的电容量均选此电容量的十倍。
2.7工作在连续模式的负输出罗氏三举变换器设计
实例
这里给出两个实例供参考。
2.7.1输出电流可变
技术要求:VI=24V,VO=144V和IO=0.2-2.0A。
解:电压传输增益M=VO/VI=6,因此k=1-3/M=0.5。
源电流II=MIO,因此IImin=6×0.2=1.2A,
IImax=6×2=12A。
我们作进一步计算时要用到的负载电阻为:Rmin=144/2=72Ω,Rmax=144/0.2=720Ω。
选斩波频率f=50kHz。由方程(32)可得:L11min=288μH。选L11=600μH,则L11=L13=L14=L12=600μH。
由方程(33)可得:C10-min=0.8μF。电容C11和C10选同一电容量,即C11=C10=4.7μF。电容C11和C10的耐压选 250V。电容C12,C13和C14选电容C10电容量的十倍,即C12=C13=C14=47μF。电容C12,C13和C14的耐压选30V。
VD11M=VD21M=VD22M=VI/(1-k)=48V。
VD23M=VD12M=2VI/(1-k)=96V;
VD13M=3VI/(1-k)=144V;VD10M=VO=144V,
ID10M=IL11M=II/3+kTVI/2L11=4.04A。
二极管全部选超快恢复二极管BYQ28E-200,其参数为:IF=10A;IFSM=50A;trr=25ns;VF=0.895V;VRRM=200V。
经计算,就可得出下列数据:
ξ1=ξ2=ξ3=0.05~0.5;ξ4=0.0044;σ1=σ2=σ3=0.001775~0.0175;ρ=0.01478~0.001478和ε=0.000033~0.0000033。
2.7.2输出电压可变:
技术要求:VI=24V,VO=96~240V和R=50Ω。
解:电压传输增益:Mmin=96/24=4和Mmax=240/24=10,因此k=0.25~0.7。输出电流IO=1.912~4.8A。
源电流IImin=1.92×4=7.68A,IImax=4.8×10=48A。
选斩波频率f=50kHz。用k=1/4,M=4代入方程(32)可得:L11min=23μH。
选L11=L13= L14=100μH=L12,用k=0.7,代入方程(33)可得:C10-min=0.83μF。电容 C11和C10选同一电容量,即C11=C10=2μF。电容C11和C10的耐压选300V。电容C12、C13和C14选电容C10电容量的十倍,即 C12=C13=C14=20μF。电容C12,C13和C14的耐压选30V。
VD11M=VD21M=VD22M=VI/(1-k)=48V。
VD23M=VD12M=2VI/(1-k)=96V;
VD13M=3VI/(1-k)=144V;VD10M=VO=240V,
ID10M=IL11M=II/3+kTVI/2L11=16+0.7×2.4=17.68A。
二极管选快恢复二极管BYT30P-400,其参数为:IF=30A;trr=50ns;VRRM=400V。将M和k代入有关式中,就能得出下列数据:
ξ1=ξ2=ξ3=0.105~0.234;ξ4=0.0312~0.0875;σ1=σ2=σ3=0.04~0.1;
ε=0.0000078~0.0000218
